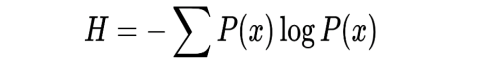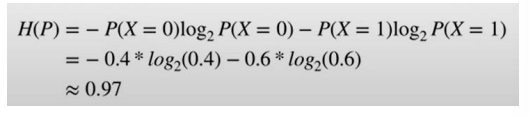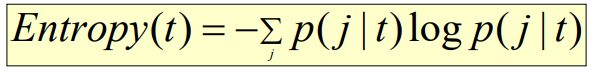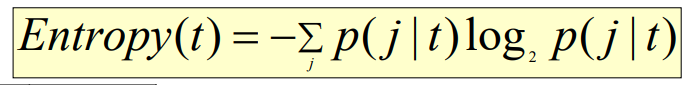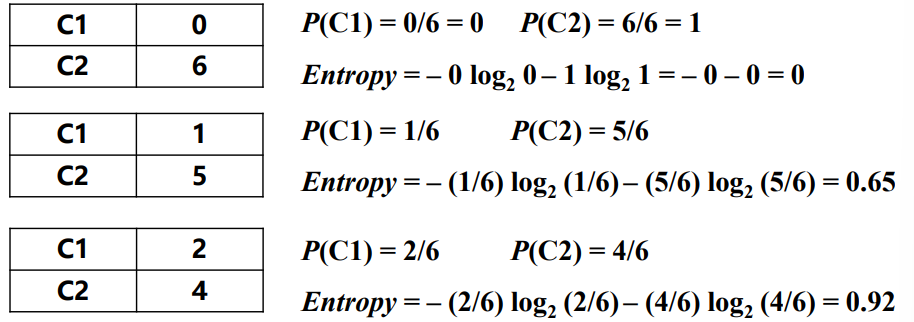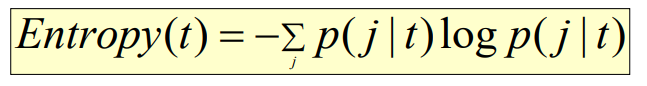数据离散化处理方法_熵值法通俗易懂介绍「建议收藏」

数据离散化

• 数据离散化
  • 连续数据过于细致，数据之间的关系难以分析
  • 划分为离散化的区间，发现数据之间的关联，便于算法处理
    • 同学们成绩：100分制分数使用五分制离散化表示
      • A（大于等于85分），B，C，D，F（小于60分）
    • 人的年龄：离散化为不同的年龄段（引源自世卫组织）
      • 未成年人：0至17岁；
      • 青年人：18岁至45岁；
      • 中年人：46岁至69岁；
      • 老年人：大于70岁。
    • 一年365天：离散化表示为12个月份或四个季节
  • 

非监督离散化

• 分箱
  1. 排序数据，并将他们分到等深的箱中
  2. 按箱平均值平滑、按箱中值平滑、按箱边界平滑等
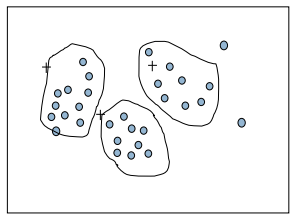
• 聚类：监测并且去除噪声数据
  • 将类似的数据聚成簇
  • 每个簇计算一个值用以将该簇的数据离散化

有监督离散化

有监督离散化—基于熵的离散化

• 熵用来度量系统的不确定程度
  • 熵是由 克劳德·艾尔伍德·香农 将热力学的熵，引入到信息论，因此它又被称为香农熵
  • 香农提出了信息熵的概念，为信息论和数字通信奠定了基础，被誉为“信息论之父”

信息熵

• 信息熵：度量系统的不确定程度
  • 信息量
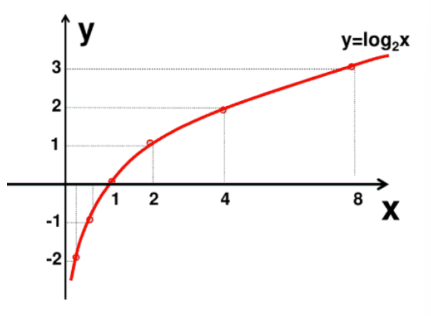
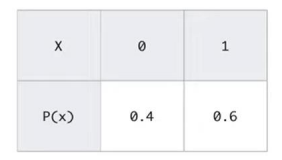
    • 定义一个事件x的概率分布为P(x)
    • 则事件x的自信息量是-logP(x), 取值范围:[0,+∞]
• 信息熵
  • 平均而言，发生一个事件我们得到的自信息量大小
  • 即：熵可以表示为自信息量的期望
    

熵与数据离散化

• 熵与数据离散化有什么关系？——不确定程度
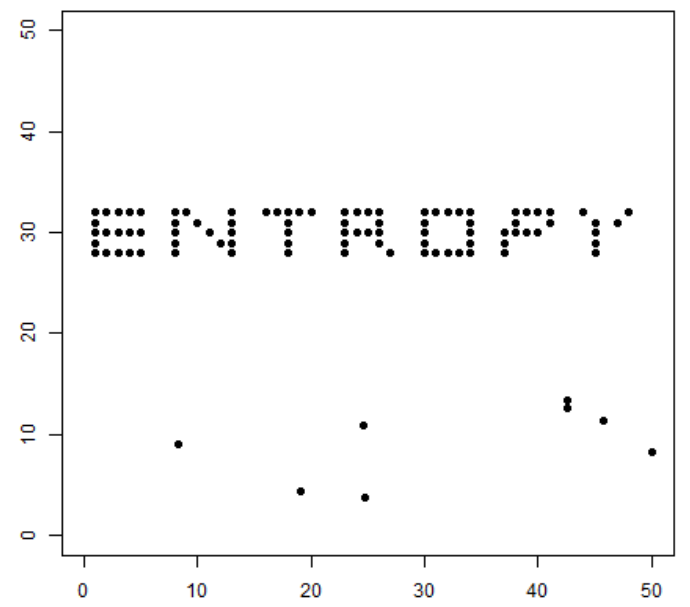
  • 数据点单词（ENTROPY）完整的时候，容易理解表达的意思，确定程度较高，对应的信息熵也较小。
  • 数据点被完全打乱的时候，难以理解其意思，造成不确定性也就多了，对应的信息熵也变大了。
  • 目标：对数据进行离散化后，每个区间的数据的确定性（又称“纯度”）更高，因此用熵来对数据进行离散化。

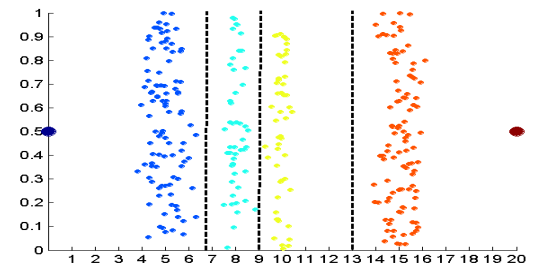
基于熵的离散化

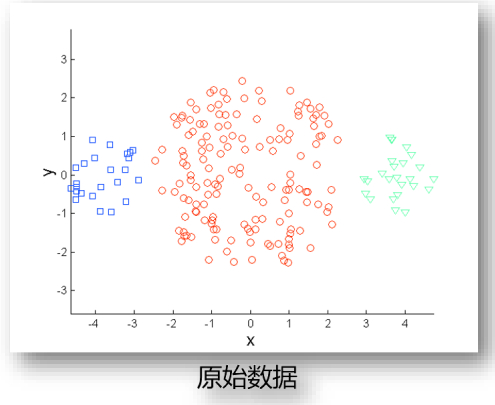
• 在x轴上对数据划分
• 熵—计算不确定性以及不纯性
  • 假设数据已经离散，计算离散后的某个区间 t 中的熵:
• 其中，p( j | t) 表示 第 j 类在区间 t 中的概率；一般对数log以2为底
• 计算 单个区间 的 Entropy
• 熵—计算不确定性以及不纯性
  • 假设数据已经离散，计算离散后的某个区间 t 中的熵
    • 其中，p( j | t) 表示 第 j 类在区间 t 中的概率；一般对数log以2为底
• 

今天的文章数据离散化处理方法_熵值法通俗易懂介绍「建议收藏」分享到此就结束了，感谢您的阅读。