python区间估计_函数的最大值和最小值怎么求

区间最大值

题目描述
给定一个长度为 N 的数组 a，其值分别为 a1,a2,...,aN

现有 Q 个询问，每个询问包含一个区间，请回答该区间的最大值为多少。

输入描述
输入第 1 行包含两个正整数N,Q，分别表示数组a的长度和询问的个数。

第 2 行包含 N 个非负整数 a1,a2,...,aN，表示数组a元素的值。

第 3∼Q+2 行每行表示一个询问，每个询问包含两个整数L,R表示区间的左右端点

1≤N,Q≤5×10^5,1≤l≤r≤N,−10^9≤ai≤10^9
 

输出描述
输出共 Q 行，每行包含一个整数，表示相应询问的答案。

输入输出样例
示例 1
输入

5 5
1 2 3 4 5
1 1 
1 2 
1 3
3 4
2 5

输出

1
2
3
4
5

运行限制
最大运行时间：3s
最大运行内存: 512M

分析

• 一看数据规模就知道不可能用暴力来做。复杂度为O(m+n)

• 求区间最值问题（RMQ问题），一般使用ST算法来做，但ST算法预处理的时间为O(nlogn)，查询为O(1)

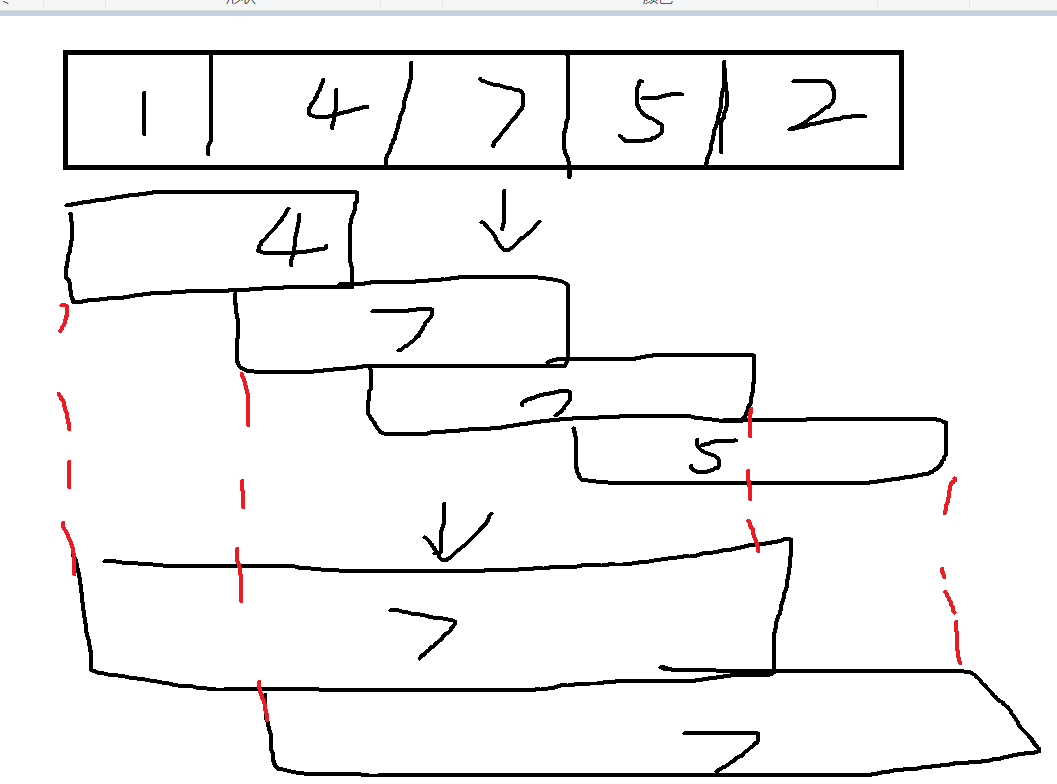
• dp[i][k]表示左端点为i,区间长度为2^k的最值，该题目是最大值。过程类似这样：
  

• 首先区间长度2^k中的k，最多为logn（向下取整），因为如果向上会出现越界问题

• 左端点肯定是从1开始（0位不计），到n+1-2^k，n-2^k是左端点到最后的区间长度，加1是左端点应从1位开始。（自己画个图就明白了），dp由区间长度为2个区间长度为k-1的区间覆盖（这里区间可能重合），第一个区间左端点为s，第二个区间左端点就为s+2^(k-1)

• 查找原理基本一致，就是找覆盖的区间

运行代码

import os
import sys


# 倍增
import math

def st():
    global n
    
    # dp初始化
    for i in range(1,n+1):
        dp[i][0] = nums[i-1]
        
    # 开始状态转移
    t = int(math.log2(n))
    for k in range(1,t+1):
        for s in range(1,n+2-pow(2,k)): # 左端点
            dp[s][k] = max(dp[s][k-1],dp[s+pow(2,k-1)][k-1])
        
def rmq(L,R):
    k = int(math.log2(R-L+1))
    return max(dp[L][k],dp[R-pow(2,k)+1][k])
        
n,q = map(int,input().split())
nums = list(map(int,input().split()))
dp = [[0]* 40 for _ in range(n+1)]
st()
for i in range(q):
    L,R = map(int,input().split())
    res = rmq(L,R)
    print(res)

通过截图

m计划

题目描述
小明是个鹅卵石收藏者，从小到大他一共收藏了 n 块鹅卵石，编号分别为 1∼n，价值分别为 a1,a2,……,an

这天他乘船准备去往蓝桥王国，然而天有不测风云，小明所在的海域下起了暴雨。

很快小明船上的积水越来越多，为了防止沉船，小明不得不选择若干块他收藏的鹅卵石丢弃。

小明制定了一套名为m计划的选择方案，其内容如下：

对于任意区间[i,i+m−1]丢弃价值最小的鹅卵石i∈[1,n−m+1]。
对于一块鹅卵石，它在 m 计划中是可以被丢弃多次的。
请你输出将被小明丢弃的鹅卵石的价值。

输入描述
输入第 1 行包含两个正整数n,m。

接下来一行包含 n 个正整 a1,a2,……,an，表示鹅卵石的价值。

1≤m≤n≤5×10^5，0≤ai≤10^9。

输出描述
输出共n−m+1行，每行输出一个整数，第i行输出整数的含义为 ai——a(i+m-1)的最小值。

输入输出样例
示例 1
输入

5 3
5 3 2 4 1

输出

2
2
1

运行限制
最大运行时间：2s
最大运行内存: 256M

分析

• 其实和上面那题是一样的，但是同样的方法在这题超时了！！！
• 题目特点，最小值由一个会滑动的窗口决定（比如2到5，下一个就3到6）
• 所以，这题用单调队列既简单复杂度又低（单调队列的经典题）
• 单调队列存储的是下标，维护的是值递增的队列。熟记公式：头尾尾头
• 头：处理头过期的下标，i-m的值为过期的下标，如果队头下标小于或等于过期下标，即需要清理（由于使用双端队列，所以可以从队头弹出）
• 尾：添加元素前检查是否要弹出，如果最后一个元素大于或者等于即将插入的数据，则从尾部弹出（注意：弹出的应该是大的元素，因为题目中要最小值）
• 尾：直接从队尾插入元素
• 头：储存或直接打印队头。首先加一个判定，保证窗口至少存在，即下标值>=窗口值-1，然后根据需要打印或者储存。

运行代码

from collections import deque

n, m = map(int, input().split())
nums = list(map(int,input().split()))

q = deque()

for i, data in enumerate(nums):
    while q and q[0] <= i - m:
        q.popleft()
    while q and nums[q[-1]] >= data:
        q.pop()
    q.append(i)
    if i >= m - 1:
        print(nums[q[0]])

通过截图

如有错误，敬请指正，欢迎交流，谢谢♪(･ω･)ﾉ

今天的文章python区间估计_函数的最大值和最小值怎么求分享到此就结束了，感谢您的阅读。