用Python学习吴恩达机器学习——梯度下降算法理论篇

开篇词：（CSDN专供）

欢迎阅读我的文章，本文起先是在B站上进行投稿，一开始是采用吴恩达机器学习2012年版的，目前已经出了十二期了。现在我决定将我摸索出来的学习笔记在各个平台上进行连载，保证同时更新。

半年已过，谁知道AI领域已发生很大的变数，近期热门的AI绘画也加剧了AI学习的需求和浪潮，现在正值吴恩达老师推出吴恩达机器学习10周年之际推出的最新版机器学习2022课程，我在观望了新旧两版课程后。果断决定跳上新版课程的列车，因为新版终于使用Python了，其开放、开源的jupyter实验室资源终于解开了我半年以来的疑惑和思路。所以让我们继续

用Python学习机器学习吧！

print(‘Python YYDS!!!’) 

目录

Gradient Descent 梯度下降(对应视频P15)

Implementing Gradient Descent 实现梯度下降(对应视频P16) 

Gradient Descent Intution 梯度下降的直觉(对应视频P17) 

Learning Rate 学习率(对应视频P18) 

本文对应以下课程视频内容“P15-P20”整编而成 

Gradient Descent 梯度下降(对应视频P15)

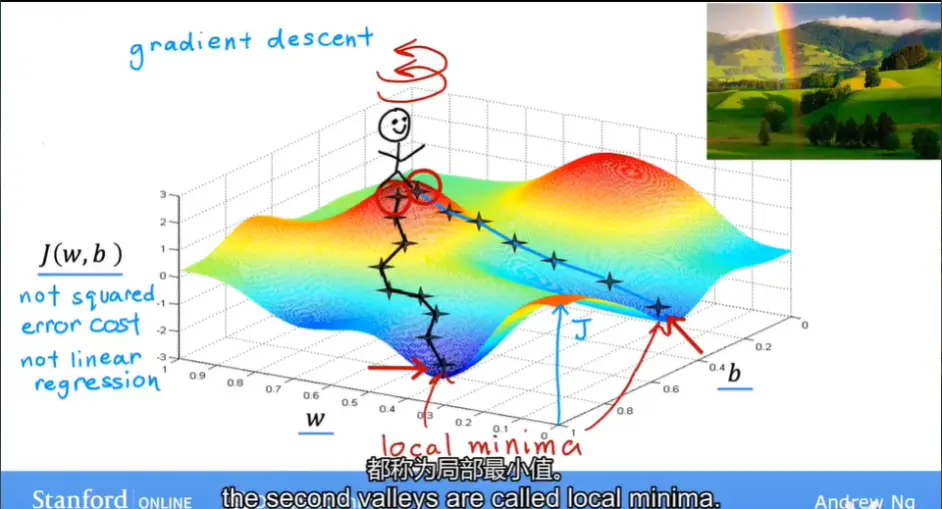
欢迎回来！在上一个视频中我们看到了成本函数J以及如何尝试选择不同的参数w和参数b并查看他们为您带来的代价函数值，如果我们有更系统的方法来找到参数w和参数b的值，那就好了，这将得到参数w,b的最小代价函数值J的结果，

 这是梯度下降算法的公式，之后会解释其含义。

        事实证明，您可以使用一种称为梯度下降的算法来做到这一点。

梯度下降算法在机器学习中无处不在，不仅用于线性回归的训练，还用于一些最先进的神经网络模型，也称深度学习模型，深度学习是您在第二门课程中学习到的，学习这两种梯度下降算法将使您拥有机器学习的重要组成部分。

        梯度下降算法可以用来尝试最小化任何函数，而不仅仅是线性回归模型的代价函数。

首先，你要做的只是开始对参数w,参数b进行预测，在线性回归中，初始值是多少并不重要，所以一个常见的选择是将所有参数都设置为0(set w=0,b=0)。

然后，您将一直更改参数w和参数b的值，以尝试降低代价函数的参数w和参数b的值。

直到代价函数J达到或接近最小值。

 下面直接给出梯度下降算法思想的直观解释图(新版课程的) 

Implementing Gradient Descent 实现梯度下降(对应视频P16) 

让我们看看如何在实际中实现梯度下降算法，让我写一下梯度下降算法 

注意：这里的“=”不是数学意义上的“等于号”，而是之前我们学过的赋值的意思，即将“=”号右边的计算结果赋值给“=”左边。式子中“α”是希腊字母Alpha代表学习率(Learning Rate)

如果学习率alpha非常大，那您下山会非常激进，你会试图下坡时迈太大的步子(容易扯到egg)

如果学习率alpha非常小，那您下山会非常“淑女”，你将迈小步下坡。下篇我们会回来解释如何选择一个较好的学习率，让您安稳下山。

最后，关于标红的这一坨东西，是代价函数J的导数项 

现在，我想提下，导数来自微积分，即使你不熟悉微积分，也不用担心。接下来给出参数b的算法 

 最后给出梯度下降算法的全公式 

        对于梯度下降算法，您将重复这两个更新步骤，直到算法收敛(指到达一个局部最小值的点)，参数w和参数b不在随着您采取每个额外步骤而发生很大的变化。

一个重要的细节是，对于梯度下降，您要同时更新参数w和参数b 

左边的做法是正确的，要同时更新参数w,b

Gradient Descent Intution 梯度下降的直觉(对应视频P17) 

现在让我们更深入地研究梯度下降以获得更好的直觉，这是上一篇你看到的梯度下降算法 

        按照数学惯例，这里的d是用这种有趣的字体写的，如果你有一定的数学基础，你应该知道这不是导数，是偏导数。但是为了实现机器学习算法，这里将其称为导数。我们现在要关心的是这套公式是什么意思，怎么来的？为什么要这样相乘，它导致了参数w和参数b的更新。

        假设你现在有这个代价函数J，你也使用这种算法试图通过调整参数w来最小化代价函数值

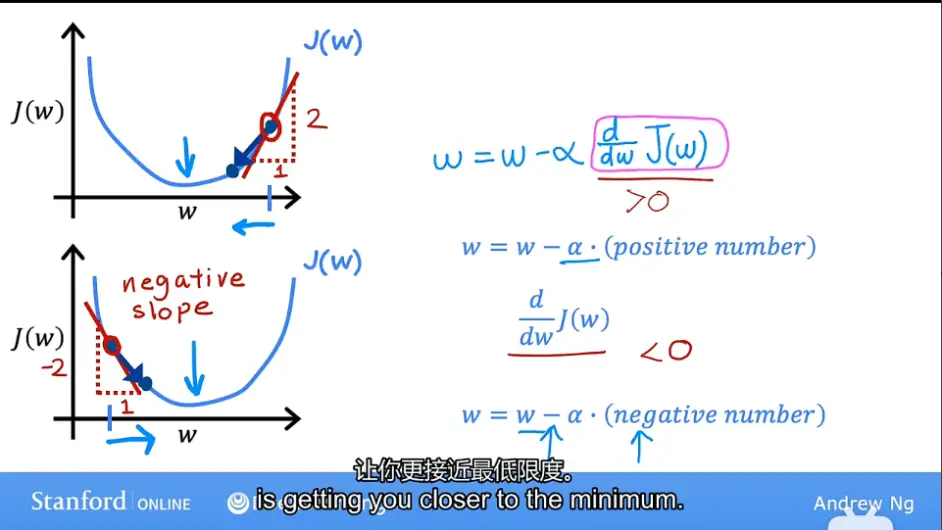
现在我们把难度降低点，只考虑一个参数的情况，先暂时将参数b的值设成0，这样就是个二维图像，而不是三维图像了，让我们看看梯度下降中代价函数J对参数w的作用 

        这里是斜率，代入到上文提到的(1)式中，因为看图像，这个导数是一个正数所以大于0，所以最新更新的参数w值是参数w值-学习率乘以某个正数。那你会得到一个更小的参数w值，在图像上的体现就是，点正在向左移动，参数w数值正在减少

稍微总结一下就是以下式子 

0\\ &w=w-\alpha(positive \,\,number)\\ &w=w-\alpha\frac{\partial}{\partial w}J(w)<0\\ &w=w-\alpha(negative \,\,number)\\ \end{aligned}">

这篇的目的是能让你理解为什么梯度下降中的导数是有意义的，梯度下降算法中的另一个关键因素是学习率Alpha,你如何选择Alpha,你如何选择Alpha?如果它太大会发生什么？

Learning Rate 学习率(对应视频P18) 

        学习率alpha的选择将对您实现梯度下降的效率产生巨大影响，学习率alpha的选择至关重要。在本篇中，让我们更深入地了解学习率，这也将帮助您实现梯度下降算法。

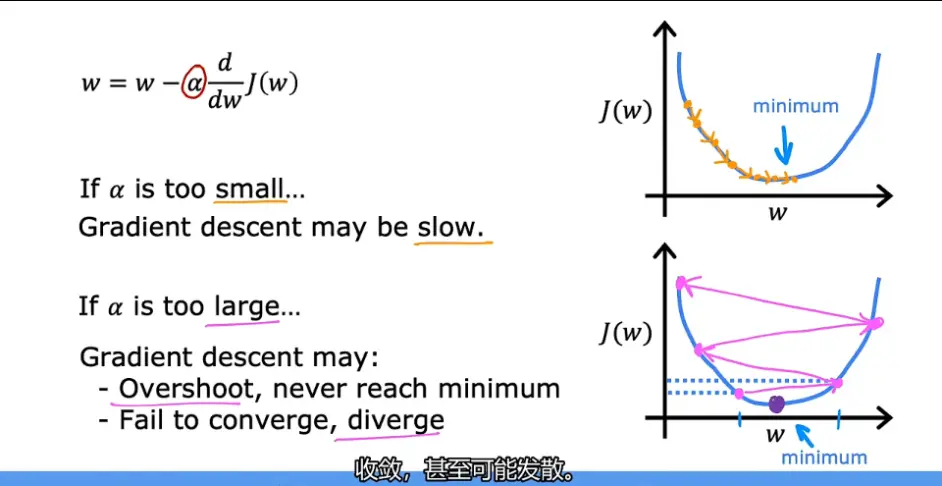
上图可以看到学习率的选取对梯度下降算法的效率有很大的影响，稍微总结一下吧

if α is too small…
如果学习率α太小的话
Gradient        descent may be slow.
梯度下降过程会很慢

if α is too large…
如果学习率α太大的话
Gradient        descent may:
Overshoot,never reach minimum，Fail to converge,diverge
梯度下降过程会很冲，并从不到达最小值,无法收敛，甚至发散 

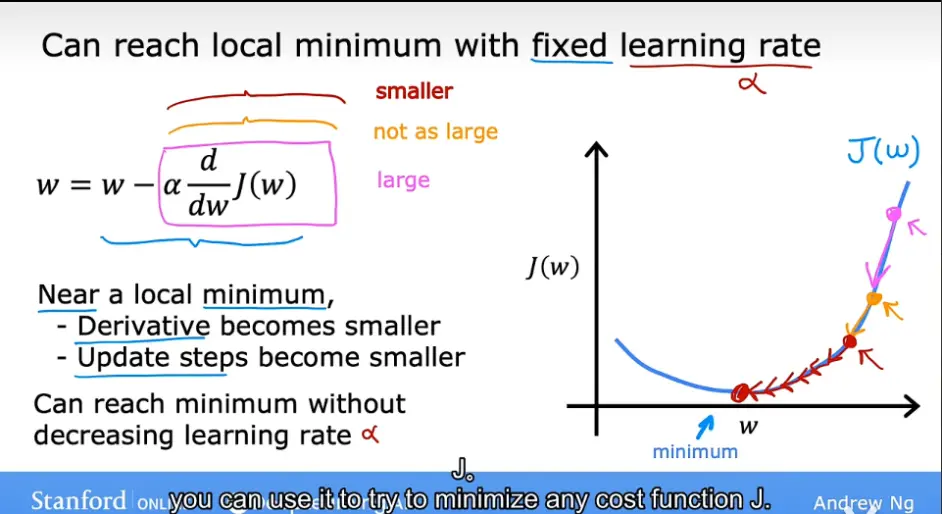
        现在我们就可以用J函数进行梯度下降了，如图，一开始第一步到第二步迈的很大，不断进行的过程中，每一步的间隔越来越小直至接近局部最小值。

        在下一篇笔记中，我们将采用函数J并将使用线性回归模型的代价函数中，这就是第一个学习的算法——线性回归算法。 

        之所以没在这里使用Python解释是因为上面吴老师所列举的J函数还没有具体的式子，不好编写，只能说写伪代码，所以在下一篇笔记中，我们会重新定义之前实现的线性函数代码！

在下一篇笔记里，我们将会用Python带入到线性函数中，这样才便于理解，敬请期待吧！

Author: Andrew Ng

Editor:  Phoenix fight!

Date：2022 Oct 14th  

免责声明！！！

关于封面图是由AI生成，以下是AI生成的图片的服务免责声明，望周知！

如有疏漏欢迎前往评论区提出并指正！

一起学习，一起进步，一起分享，一起成长！

最后欢迎各位前往我的B站专栏阅读往期文章，

https://www.bilibili.com/read/cv19090716

顺便吐槽一下，CSDN你们的Latex编辑器居然不支持中文？

今天的文章用Python学习吴恩达机器学习——梯度下降算法理论篇分享到此就结束了，感谢您的阅读。