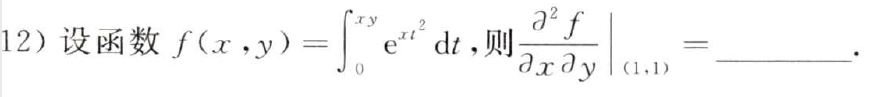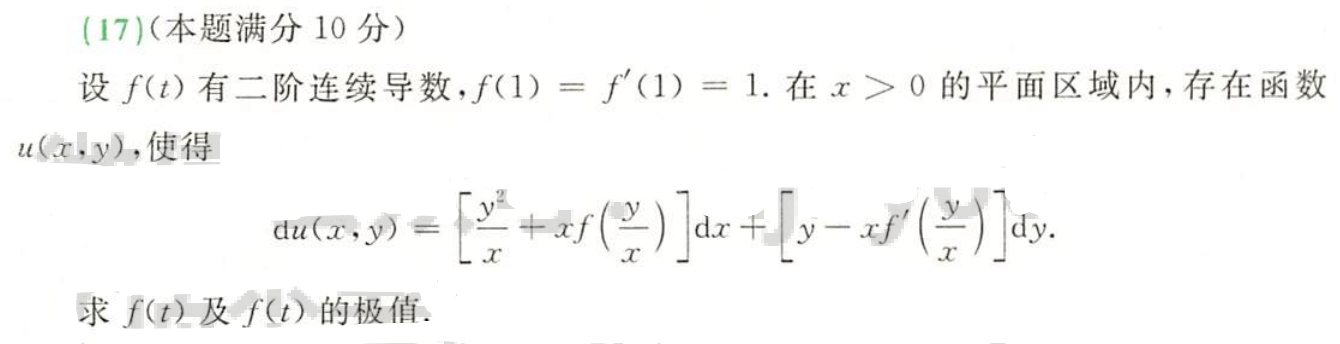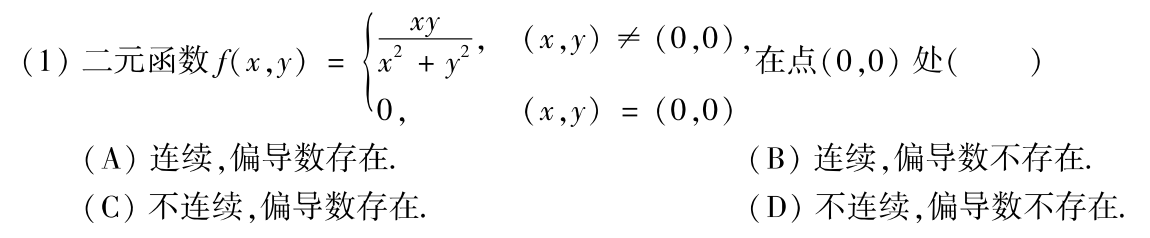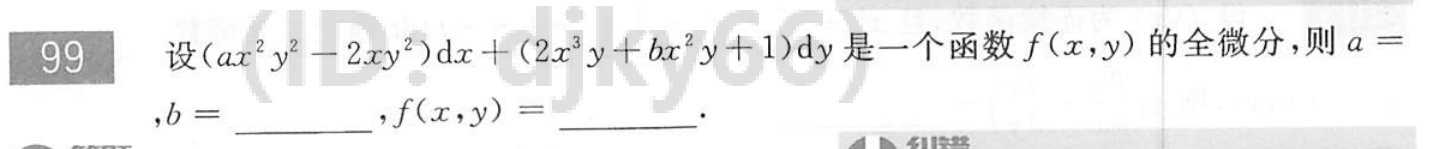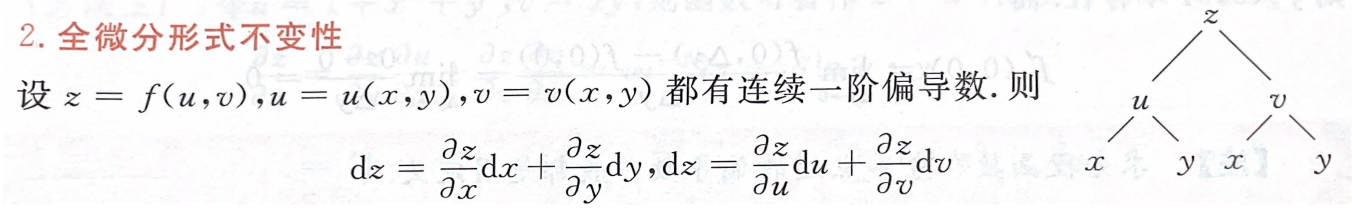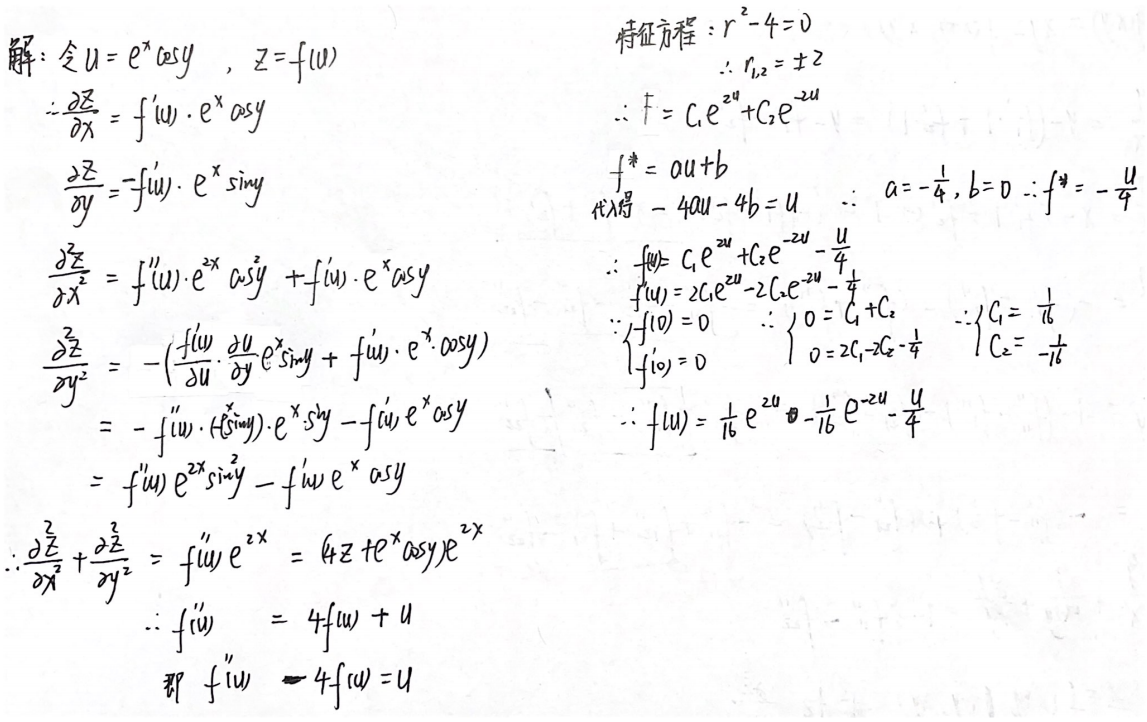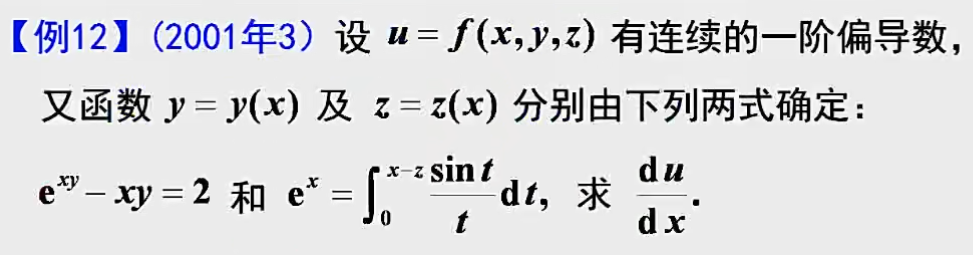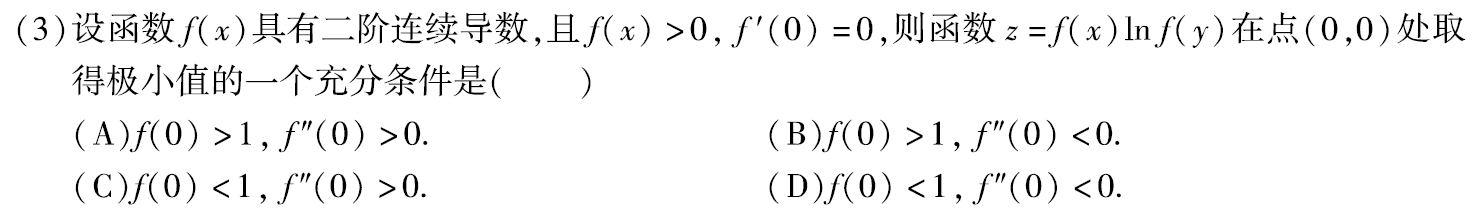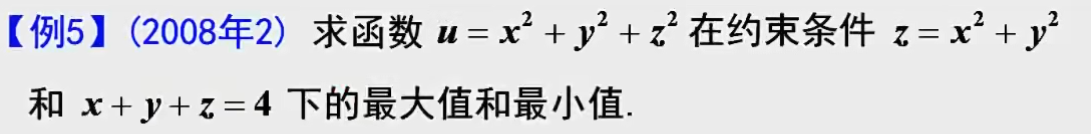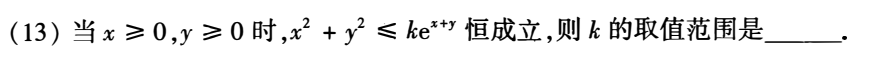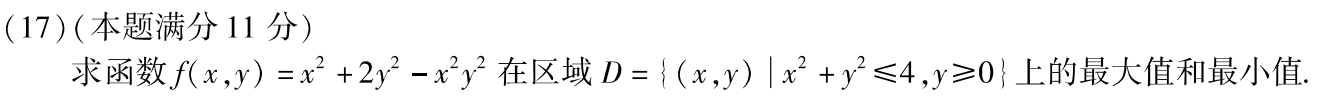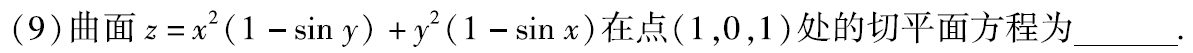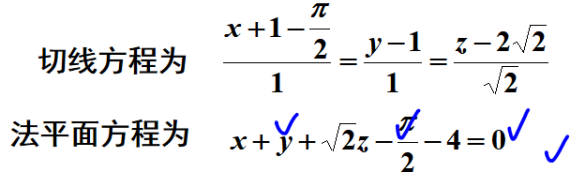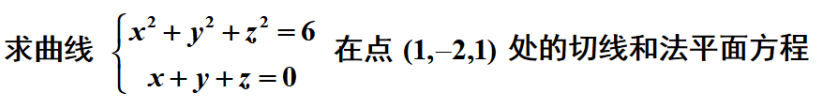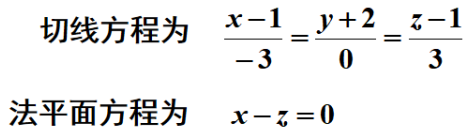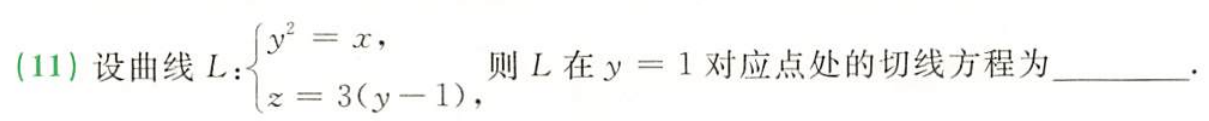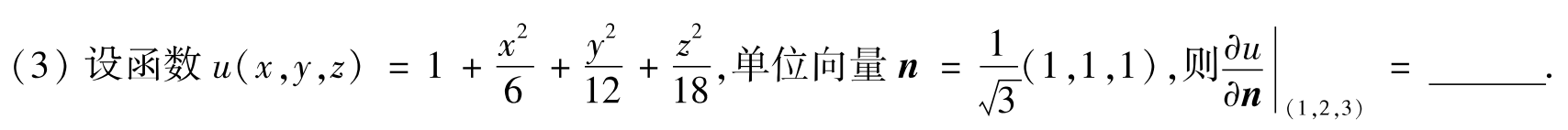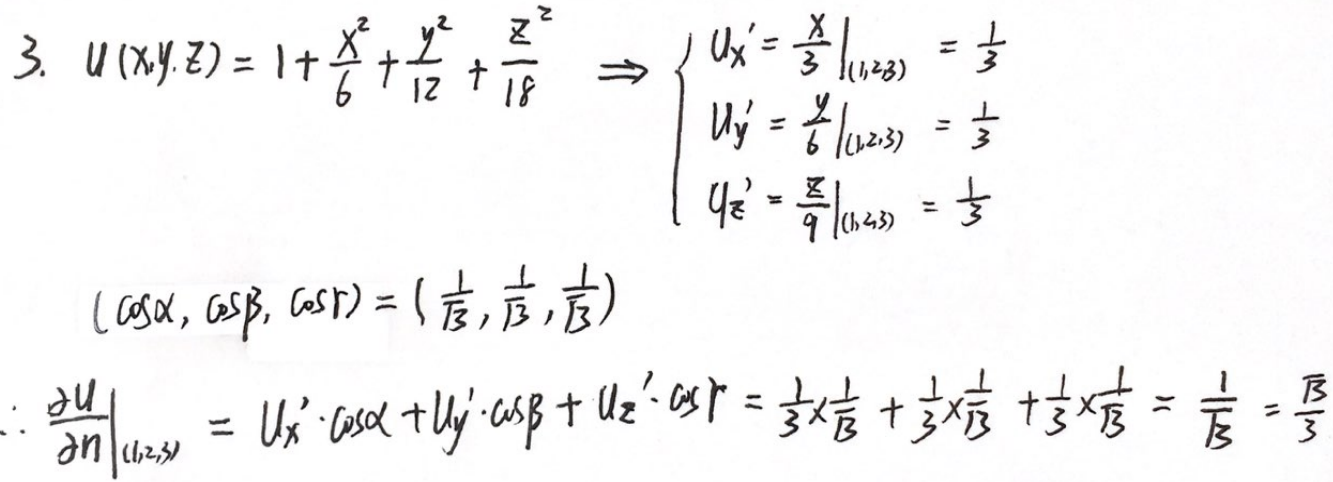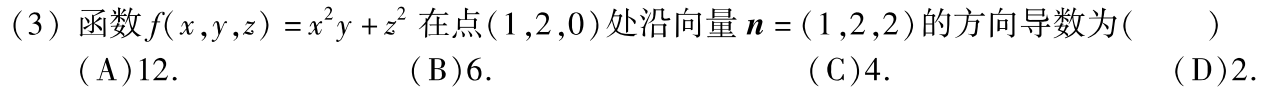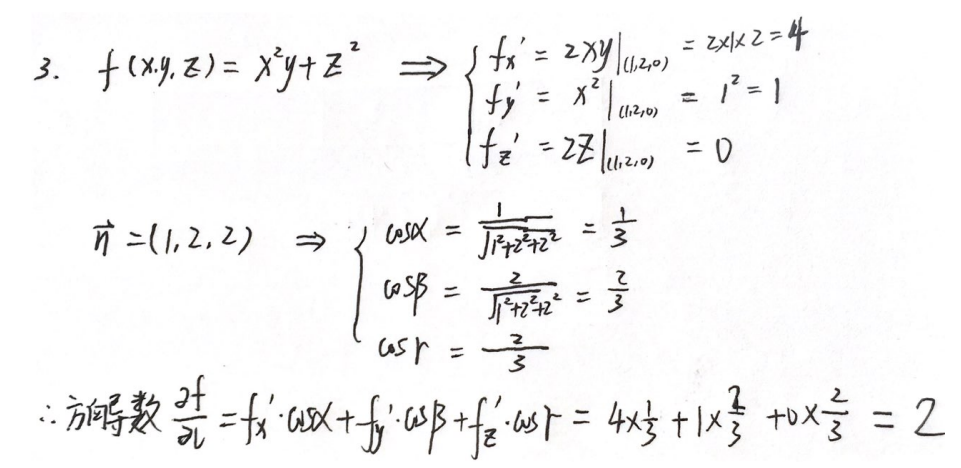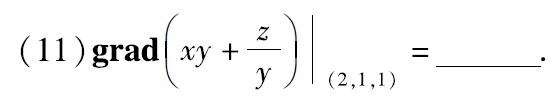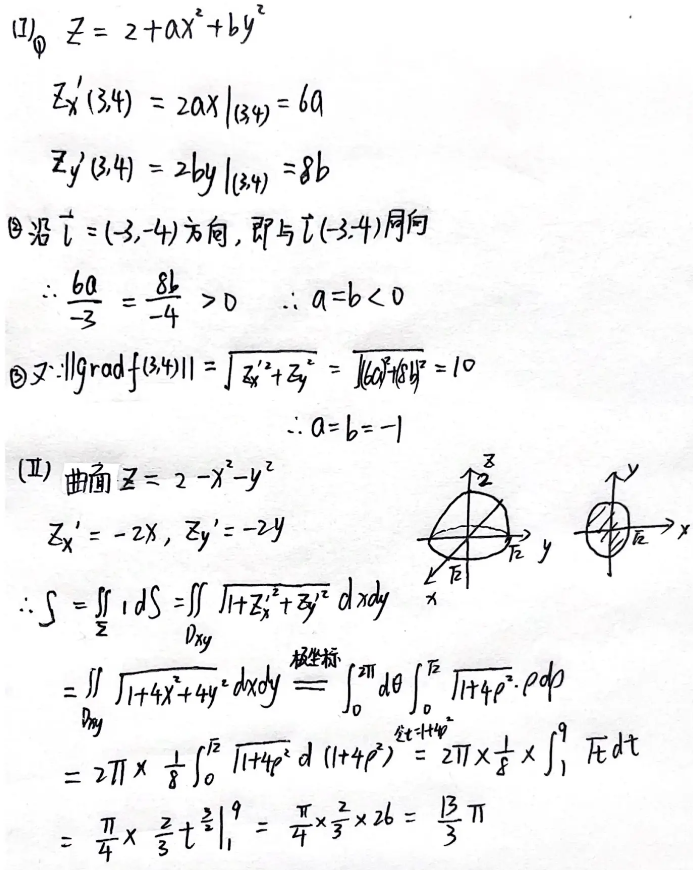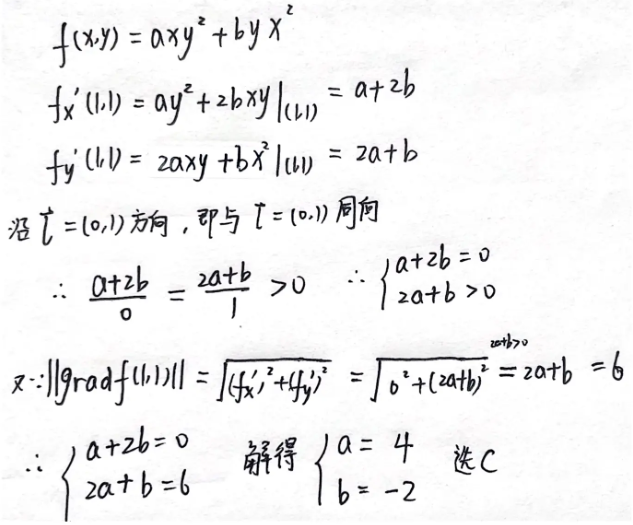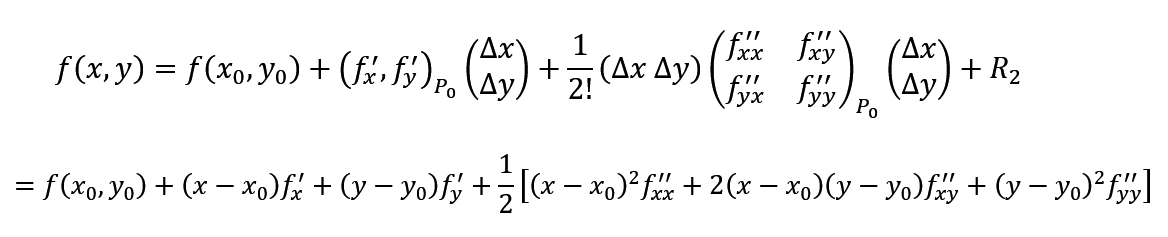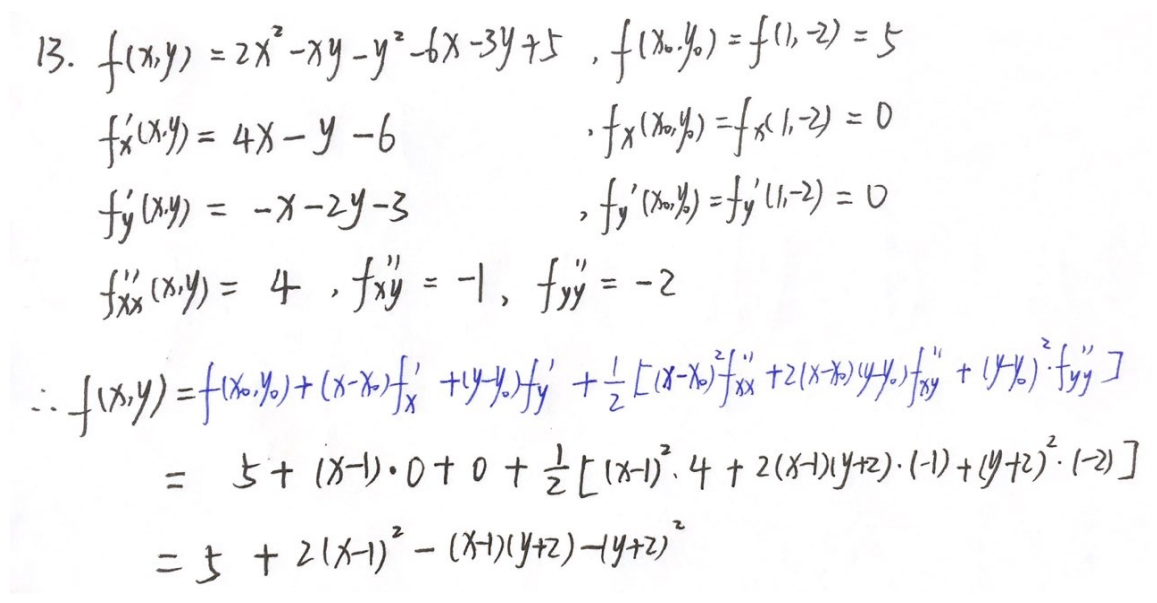文章目录
Ch9. 多元函数微分学 及其应用
1.(第一节)多元函数的基本概念:重极限、连续、偏导数、全微分
2.(第二节) 多元函数的微分法:偏导数与全微分的计算:复合函数微分法、隐函数微分法
3.(第三节) 多元函数的应用:极值与最值、方向导数与梯度、曲面的切平面和法线、曲线的切线和法平面
(一) 重极限
二重极限:二元函数的极限
两类题型:【高数辅导讲义P143 例1 例2】
1.求重极限:
一般方法:取绝对值 |f(x,y)|,用夹逼原理
2.证明重极限不存在:
取特殊路径:
①一般取直线 y=kx,重极限与k有关
②沿两个不同路径极限不同
(二) 多元函数的连续性
lim x → x 0 y → y 0 f ( x , y ) = f ( x 0 , y 0 ) \lim\limits_{x→x_0 \atop y→y_0}f(x,y)=f(x_0,y_0) y→y0x→x0limf(x,y)=f(x0,y0)
连续的必要条件(前提):极限存在
连续的充要条件:极限存在,且等于函数值
(三) 偏导数
1.偏导数的定义
1.对x的偏导数:
若 lim Δ x → 0 f ( x 0 + Δ x , y 0 ) − f ( x 0 , y 0 ) Δ x = d d x f ( x , y 0 ) ∣ x = x 0 \lim\limits_{Δx→0}\dfrac{f(x_0+Δx,\ y_0)-f(x_0,y_0)}{Δx}=\dfrac{d}{dx}f(x,y_0)|_{x=x_0} Δx→0limΔxf(x0+Δx, y0)−f(x0,y0)=dxdf(x,y0)∣x=x0存在,则记为 ∂ f ∂ x ∣ x = x 0 , y = y 0 \dfrac{∂f}{∂x}|_{x=x_0,y=y_0} ∂x∂f∣x=x0,y=y0或 f x ′ ( x 0 , y 0 ) f’_x(x_0,y_0) fx′(x0,y0)
2.对y的偏导数:
若 lim Δ y → 0 f ( x 0 , y 0 + Δ y ) − f ( x 0 , y 0 ) Δ y = d d y f ( x 0 , y ) ∣ y = y 0 \lim\limits_{Δy→0}\dfrac{f(x_0\ ,y_0+Δy)-f(x_0,y_0)}{Δy}=\dfrac{d}{dy}f(x_0,y)|_{y=y_0} Δy→0limΔyf(x0 ,y0+Δy)−f(x0,y0)=dydf(x0,y)∣y=y0存在,则记为 ∂ f ∂ y ∣ x = x 0 , y = y 0 \dfrac{∂f}{∂y}|_{x=x_0,y=y_0} ∂y∂f∣x=x0,y=y0或 f y ′ ( x 0 , y 0 ) f’_y(x_0,y_0) fy′(x0,y0)
2.偏导数的几何意义:切线对x轴和y轴的斜率
1. f x ′ ( x 0 , y 0 ) f’_x(x_0,y_0) fx′(x0,y0):表示曲线 z = f ( x , y 0 ) z=f(x,y_0) z=f(x,y0) 在点 ( x 0 , y 0 , f ( x 0 , y 0 ) ) (x_0,y_0,f(x_0,y_0)) (x0,y0,f(x0,y0))处的切线对 x x x轴的斜率
2. f y ′ ( x 0 , y 0 ) f’_y(x_0,y_0) fy′(x0,y0):表示曲线 z = f ( x 0 , y ) z=f(x_0,y) z=f(x0,y) 在点 ( x 0 , y 0 , f ( x 0 , y 0 ) ) (x_0,y_0,f(x_0,y_0)) (x0,y0,f(x0,y0))处的切线对 y y y轴的斜率
3.偏导数的计算:
(1)用偏导数的定义求
(2)先代后求
具体函数在具体点求偏导数,可以先代后求
例如:
一阶偏导数: f x ′ ( 0 , 0 ) = d d x f ( x , 0 ) ∣ x = 0 f’_x(0,0)=\dfrac{d}{dx}f(x,0)|_{x=0} fx′(0,0)=dxdf(x,0)∣x=0, f y ′ ( 0 , 0 ) = d d y f ( 0 , y ) ∣ y = 0 f’_y(0,0)=\dfrac{d}{dy}f(0,y)|_{y=0} fy′(0,0)=dydf(0,y)∣y=0 【讲义P152例2】
二阶偏导数,求最后一阶时先代后求:求 ∂ 2 z ∂ x ∂ y ∣ ( 0 , 1 ) \dfrac{∂^2z}{∂x∂y}|_{(0,1)} ∂x∂y∂2z∣(0,1)
先求出 ∂ z ∂ x \dfrac{∂z}{∂x} ∂x∂z,则 ∂ 2 z ∂ x ∂ y = d d y ( ∂ z ( 0 , y ) ∂ x ) ∣ y = 1 \dfrac{∂^2z}{∂x∂y}=\dfrac{d}{dy}(\dfrac{∂z(0,y)}{∂x})|_{y=1} ∂x∂y∂2z=dyd(∂x∂z(0,y))∣y=1 【讲义P152例3】
原理:
偏导数,本质上就是一元函数的导数:
① f x ′ ( x 0 , y 0 ) f’_x(x_0,y_0) fx′(x0,y0)就是一元函数 f ( x , y 0 ) f(x,y_0) f(x,y0)在 x 0 x_0 x0处的导数
② f y ′ ( x 0 , y 0 ) f’_y(x_0,y_0) fy′(x0,y0)就是一元函数 f ( x 0 , y ) f(x_0,y) f(x0,y)在 y 0 y_0 y0处的导数
由此可以“先代后求”
先代后求的原理:偏导数本质上是一元函数的导数
4.高阶偏导数
(1)二阶混合偏导数相等
定理:若函数z=f(x,y)的两个二阶混合偏导数 ∂ 2 z ∂ x ∂ y \dfrac{∂²z}{∂x∂y} ∂x∂y∂2z及 ∂ 2 z ∂ y ∂ x \dfrac{∂²z}{∂y∂x} ∂y∂x∂2z在区域D内连续,则在区域D内这两个二阶混合偏导数必相等:
∂ 2 z ∂ x ∂ y \dfrac{∂²z}{∂x∂y} ∂x∂y∂2z及 ∂ 2 z ∂ y ∂ x \dfrac{∂²z}{∂y∂x} ∂y∂x∂2z在D内连续 ⇨ D内 ∂ 2 z ∂ x ∂ y = ∂ 2 z ∂ y ∂ x \dfrac{∂²z}{∂x∂y}=\dfrac{∂²z}{∂y∂x} ∂x∂y∂2z=∂y∂x∂2z( f 12 ′ ′ = f 21 ′ ′ f”_{12}=f”_{21} f12′′=f21′′ )
例题1:20年12. 二阶混合偏导相等
分析:
先求 ∂ f ∂ y \dfrac{∂f}{∂y} ∂y∂f,再对x求偏导
答案:4e
例题2:23李林四(一)17. ①二阶混合偏导数相等 ②微分方程(可降阶→一阶非线性) ③极值
答案:
例题3:24李林六(四)13. 二阶混合偏导数相等
分析:
由二阶混合偏导相等,得 k = − 1 k=-1 k=−1
答案:1
5.偏导连续
lim x → x 0 y → y 0 f x ′ ( x , y ) = f x ′ ( x 0 , y 0 ) \lim\limits_{x→x_0 \atop y→y_0}f’_x(x,y)=f’_x(x_0,y_0) y→y0x→x0limfx′(x,y)=fx′(x0,y0)
lim x → x 0 y → y 0 f y ′ ( x , y ) = f y ′ ( x 0 , y 0 ) \lim\limits_{x→x_0 \atop y→y_0}f’_y(x,y)=f’_y(x_0,y_0) y→y0x→x0limfy′(x,y)=fy′(x0,y0)
(四) 二元可微、全微分
1.全微分的定义
若函数 z = f ( x , y ) z=f(x,y) z=f(x,y)在点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)的全增量 Δ z = f ( x , y ) − f ( x 0 , y 0 ) = f ( x 0 + Δ x , y 0 + Δ y ) − f ( x 0 , y 0 ) Δz=f(x,y)-f(x_0,y_0)=f(x_0+Δx,y_0+Δy)-f(x_0,y_0) Δz=f(x,y)−f(x0,y0)=f(x0+Δx,y0+Δy)−f(x0,y0)
可表示为
Δ z = A Δ x + B Δ y + o ( ρ ) , Δz=AΔx+BΔy+o(ρ), Δz=AΔx+BΔy+o(ρ),
其中,A和B不依赖于Δx和Δy而仅与x和y有关, ρ = ( Δ x ) 2 + ( Δ y ) 2 ρ=\sqrt{(Δx)^2+(Δy)^2} ρ=(Δx)2+(Δy)2
则称函数 z = f ( x , y ) z=f(x,y) z=f(x,y) 在点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0) 可微, A Δ x + B Δ y AΔx+BΔy AΔx+BΔy 称为函数 z = f ( x , y ) z=f(x,y) z=f(x,y) 在点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0) 的全微分,记为
d z = A Δ x + B Δ y dz=AΔx+BΔy dz=AΔx+BΔy
全增量: Δ z = f ( x + Δ x , y + Δ y ) − f ( x , y ) Δz=f(x+Δx,y+Δy)-f(x,y) Δz=f(x+Δx,y+Δy)−f(x,y)
全微分对应全增量,偏导数对应偏增量
等价定义
注:
① A = f x ′ ( x 0 , y 0 ) , B = f y ′ ( x 0 , y 0 ) A=f’_x(x_0,y_0),B=f’_y(x_0,y_0) A=fx′(x0,y0),B=fy′(x0,y0)
② x = x 0 + Δ x , y = y 0 + Δ y x=x_0+Δx,y=y_0+Δy x=x0+Δx,y=y0+Δy
③ ρ = ( Δ x ) 2 + ( Δ y ) 2 ρ=\sqrt{(Δx)^2+(Δy)^2} ρ=(Δx)2+(Δy)2
④ d z = A Δ x + B Δ y dz=AΔx+BΔy dz=AΔx+BΔy
⑤ Δ z = d z + o ( ρ ) Δz=dz+o(ρ) Δz=dz+o(ρ)
故 Δ z = d z + o ( ρ ) = A Δ x + B Δ y + o ( ρ ) = f x ′ ( x 0 , y 0 ) ( x − x 0 ) + f y ′ ( x 0 , y 0 ) ( y − y 0 ) + o ( ρ ) Δz=dz+o(ρ)=AΔx+BΔy+o(ρ)=f’_x(x_0,y_0)(x-x_0)+f’_y(x_0,y_0)(y-y_0)+o(ρ) Δz=dz+o(ρ)=AΔx+BΔy+o(ρ)=fx′(x0,y0)(x−x0)+fy′(x0,y0)(y−y0)+o(ρ)
2.可微的判定
(1)必要条件:两个偏导数 f x ′ ( x 0 , y 0 ) , f y ′ ( x 0 , y 0 ) f’_x(x_0,y_0) , f’_y(x_0,y_0) fx′(x0,y0),fy′(x0,y0) 均存在
(2)充分条件:两个偏导数 f x ′ ( x 0 , y 0 ) , f y ′ ( x 0 , y 0 ) f’_x(x_0,y_0) , f’_y(x_0,y_0) fx′(x0,y0),fy′(x0,y0) 均连续。即 lim x → x 0 y → y 0 f x ( x , y ) = f x ( x 0 , y 0 ) \lim\limits_{x→x_0\atop y→y_0}f_x(x,y)=f_x(x_0,y_0) y→y0x→x0limfx(x,y)=fx(x0,y0), lim x → x 0 y → y 0 f y ( x , y ) = f y ( x 0 , y 0 ) \lim\limits_{x→x_0\atop y→y_0}f_y(x,y)=f_y(x_0,y_0) y→y0x→x0limfy(x,y)=fy(x0,y0)
(3)充分必要条件(定义):
lim Δ x → 0 Δ y → 0 Δ z − d z ρ = lim Δ x → 0 Δ y → 0 o ( ρ ) ρ \lim\limits_{Δx→0 \atop Δy→0}\dfrac{Δz-dz}{ρ}=\lim\limits_{Δx→0 \atop Δy→0}\dfrac{o(ρ)}{ρ} Δy→0Δx→0limρΔz−dz=Δy→0Δx→0limρo(ρ)
= lim ( x , y ) → ( x 0 , y 0 ) [ f ( x , y ) − f ( x 0 , y 0 ) ] − [ f x ′ ( x 0 , y 0 ) ( x − x 0 ) x + f y ′ ( x 0 , y 0 ) ⋅ ( y − y 0 ) ] ( x − x 0 ) 2 + ( y − y 0 ) 2 =\lim\limits_{(x,y)→(x_0,y_0)}\dfrac{[f(x,y)-f(x_0,y_0)]-[f’_x(x_0,y_0)(x-x_0)x+f’_y(x_0,y_0)·(y-y_0)]}{\sqrt{(x-x_0)^2+(y-y_0)^2}} =(x,y)→(x0,y0)lim(x−x0)2+(y−y0)2[f(x,y)−f(x0,y0)]−[fx′(x0,y0)(x−x0)x+fy′(x0,y0)⋅(y−y0)]
= lim Δ x → 0 Δ y → 0 [ f ( x 0 + Δ x , y 0 + Δ y ) − f ( x 0 , y 0 ) ] − [ f x ′ ( x 0 , y 0 ) ⋅ Δ x + f y ′ ( x 0 , y 0 ) ⋅ Δ y ] ( Δ x ) 2 + ( Δ y ) 2 = 0 =\lim\limits_{Δx→0 \atop Δy→0}\dfrac{[f(x_0+Δx,y_0+Δy)-f(x_0,y_0)]-[f’_x(x_0,y_0)·Δx+f’_y(x_0,y_0)·Δy]}{\sqrt{(Δx)^2+(Δy)^2}}=0 =Δy→0Δx→0lim(Δx)2+(Δy)2[f(x0+Δx,y0+Δy)−f(x0,y0)]−[fx′(x0,y0)⋅Δx+fy′(x0,y0)⋅Δy]=0
x = x 0 + Δ x x=x_0+Δx x=x0+Δx,即 Δ x = x − x 0 Δx=x-x_0 Δx=x−x0
y = y 0 + Δ y y=y_0+Δy y=y0+Δy,即 Δ y = y − y 0 Δy=y-y_0 Δy=y−y0
(1)可微的几何意义
曲面: z 1 = f ( x , y ) z_1=f(x,y) z1=f(x,y)
切平面: z 2 = f ( x 0 , y 0 ) + f x ′ ( x 0 , y 0 ) ( x − x 0 ) + f y ′ ( x 0 , y 0 ) ( y − y 0 ) z_2=f(x_0,y_0)+f’_x(x_0,y_0)(x-x_0)+f’_y(x_0,y_0)(y-y_0) z2=f(x0,y0)+fx′(x0,y0)(x−x0)+fy′(x0,y0)(y−y0)
分子:曲面与切平面之间的高度差
分母:投影的水平距离ρ
(2)二元不可微的典例: f ( x , y ) = ∣ x ∣ + ∣ y ∣ f(x,y)=|x|+|y| f(x,y)=∣x∣+∣y∣在点(0,0)处
考察 f ( x , y ) = ∣ x ∣ + ∣ y ∣ f(x,y)=|x|+|y| f(x,y)=∣x∣+∣y∣在点(0,0)处是否可微:
∵ f x ′ ( 0 , 0 ) = lim x → 0 f ( x , 0 ) − f ( 0 , 0 ) x − 0 = lim x → 0 ∣ x ∣ x f’_x(0,0)=\lim\limits_{x→0}\dfrac{f(x,0)-f(0,0)}{x-0}=\lim\limits_{x→0}\dfrac{|x|}{x} fx′(0,0)=x→0limx−0f(x,0)−f(0,0)=x→0limx∣x∣ 不存在,所以 f ( x , y ) = ∣ x ∣ + ∣ y ∣ f(x,y)=|x|+|y| f(x,y)=∣x∣+∣y∣在点(0,0)处对x的偏导数不存在。同理, f ( x , y ) = ∣ x ∣ + ∣ y ∣ f(x,y)=|x|+|y| f(x,y)=∣x∣+∣y∣在点(0,0)处对y的偏导数也不存在。由可微的必要条件知, f ( x , y ) = ∣ x ∣ + ∣ y ∣ f(x,y)=|x|+|y| f(x,y)=∣x∣+∣y∣在点(0,0)处不可微。
3.可微的计算
若 f ( x , y ) f(x,y) f(x,y)可微,则:
(1)二元全微分: d z = ∂ z ∂ x d x + ∂ z ∂ y d y dz=\dfrac{∂z}{∂x}dx+\dfrac{∂z}{∂y}dy dz=∂x∂zdx+∂y∂zdy
(2)三元全微分: d u = ∂ u ∂ x d x + ∂ u ∂ y d y + ∂ u ∂ z d z du=\dfrac{∂u}{∂x}dx+\dfrac{∂u}{∂y}dy+\dfrac{∂u}{∂z}dz du=∂x∂udx+∂y∂udy+∂z∂udz
(1)知道函数的全微分,求函数本身:偏积分、凑微分
已知 d u ( x , y ) = P ( x , y ) d x + Q ( x , y ) d y du(x,y)=P(x,y)dx+Q(x,y)dy du(x,y)=P(x,y)dx+Q(x,y)dy,求 u ( x , y ) u(x,y) u(x,y)
方法: 【高数辅导讲义P155例6】
1.偏积分:
知 ∂ u ∂ x 、 ∂ u ∂ y \dfrac{∂u}{∂x}、\dfrac{∂u}{∂y} ∂x∂u、∂y∂u: ∂ u ∂ x \dfrac{∂u}{∂x} ∂x∂u对x偏积分得u(x,y),再对y求偏导得 ∂ u ∂ y \dfrac{∂u}{∂y} ∂y∂u。两个 ∂ u ∂ y \dfrac{∂u}{∂y} ∂y∂u联立得 φ ′ ( y ) φ'(y) φ′(y),从而积分得 φ ( y ) φ(y) φ(y),从而得u(x,y)
2.凑微分:不好凑就分组凑
凑微分简单,但不通用。偏积分麻烦一些,但一定能做出来。
优先凑微分,凑不出则用偏积分。
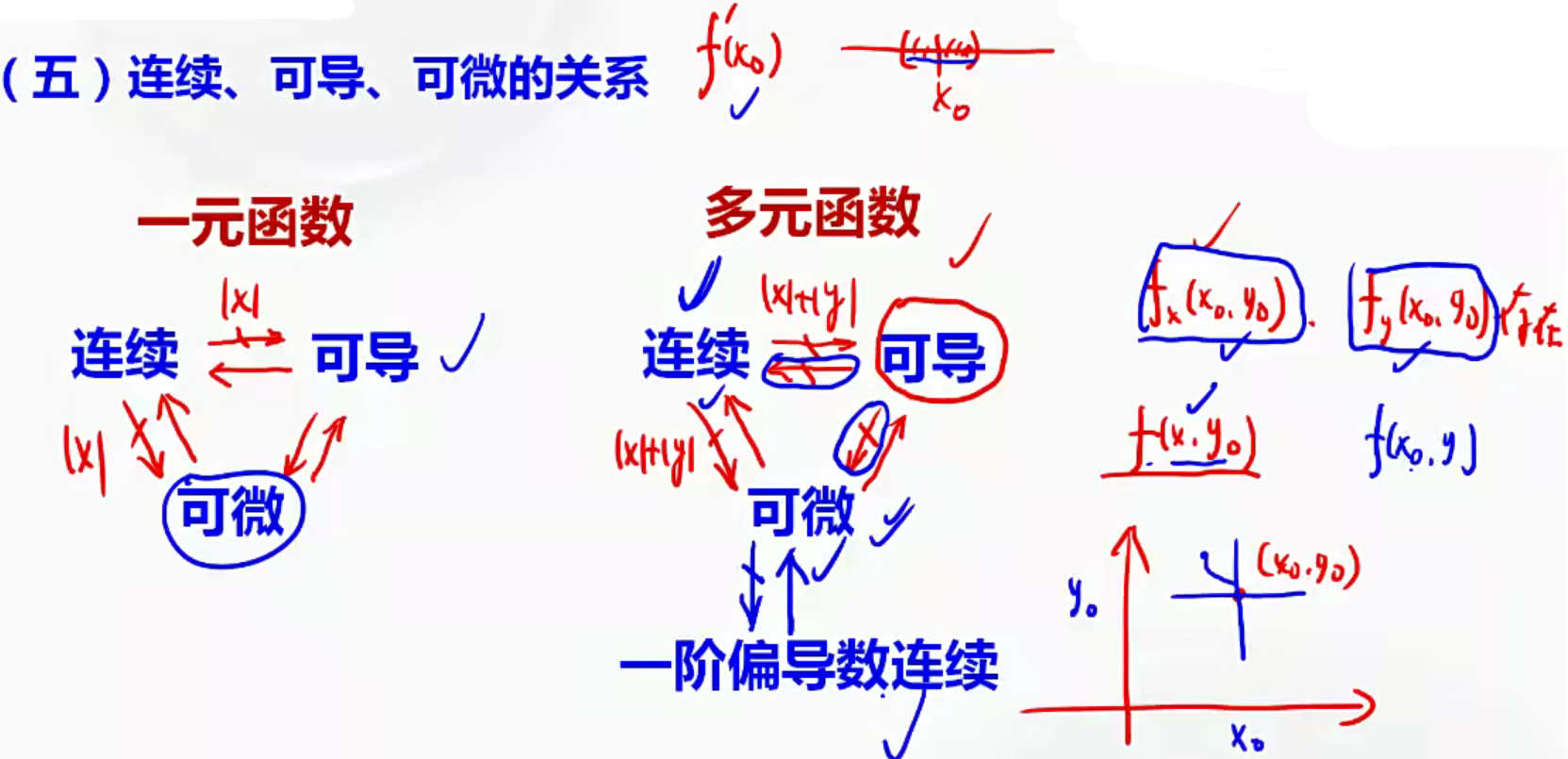
4.连续、可导、可微的关系
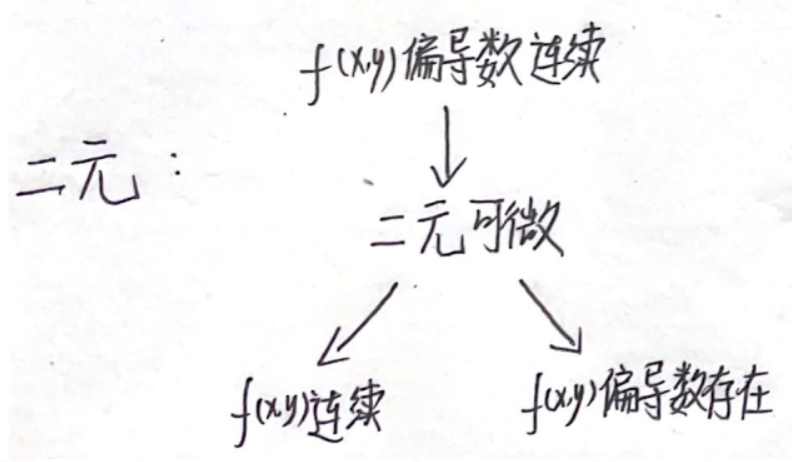
①一元和多元的差别在于:二元可导不能推二元连续。
②原因在于偏导数:二元函数可导是指f’x(x₀,y₀)、f’y(x₀,y₀)这两个偏导数存在。
偏导数只能体现 过 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)点 沿着x轴、y轴两条十字线上的函数变化率,而无法体现平面上以任意趋近的函数的变化率,所以可偏导推不出连续。(二元连续和二元可微均要求任意趋近,二元可导,即偏导,只能沿着某条线变化,本质还是一元导数)
③ f x ′ ( x 0 , y 0 ) f’_x(x_0,y_0) fx′(x0,y0)是二元函数f(x,y)对x的偏导数,可视为一元函数 f ( x , y 0 ) f(x,y_0) f(x,y0)对x的导数。
即 f x ′ ( x 0 , y 0 ) = ∂ f ( x , y ) ∂ x = d f ( x , y 0 ) d x f’_x(x_0,y_0)=\dfrac{∂f(x,y)}{∂x}=\dfrac{df(x,y_0)}{dx} fx′(x0,y0)=∂x∂f(x,y)=dxdf(x,y0) 【先代后求】
例题1:1994年
答案:D
例题2:1997年
分析:定义做
答案:C
例题3:2002年
答案:A
例4:2012年3.
分析:
答案:B
例题5:2020年3.
分析:
答案:A
例题6:24李林四(四)2.
答案:D
例题7:
例题8:660 T99 全微分
分析:全微分,则 ∂ P ∂ y = ∂ Q ∂ x \dfrac{∂P}{∂y}=\dfrac{∂Q}{∂x} ∂y∂P=∂x∂Q,求解a,b。然后用偏积分求解f(x,y)
答案: 3 , − 2 , x 3 y 2 − x 2 y 2 + y + C 3,-2,x^3y^2-x^2y^2+y+C 3,−2,x3y2−x2y2+y+C(C为任意常数)
(五) 多元复合函数 求导法则
1.复合函数求导
复合函数链导法,主要是看树状图。树状图最后有几个x,链导就是几个x相加。
要理解这种思想,而不是背公式。不同的函数的链导树状图不同,分析出来然后对照着写偏导才是正解。这样,无论多少个函数复合,复合多少层,我们都可以写出公式。
2.全微分形式不变性
多元全微分形式不变性:对z的全微分,既可以表示为对自变量x,y的偏导数和微分,也可以表示为对中间变量u,v的偏导数和微分,且全微分的形式不变。
意义:不需要区分是自变量还是中间变量
例题1:14年17.
答案:
(六) 多元隐函数 的求导公式、隐函数存在定理
三种方法:①两边求偏导 ②公式法 ③全微分形式不变性
隐函数存在定理1 (隐函数的求导公式):
F ( x , y ) = 0 , F y ( x , y ) ≠ 0 F(x,y)=0,F_y(x,y)≠0 F(x,y)=0,Fy(x,y)=0,则有 d y d x = − F x F y \dfrac{dy}{dx}=-\dfrac{F_x}{F_y} dxdy=−FyFx
隐函数存在定理2:
F ( x 0 , y 0 , z 0 ) = 0 F(x₀,y₀,z₀)=0 F(x0,y0,z0)=0, F z ′ ( x 0 , y 0 , z 0 ) ≠ 0 F’_z(x₀,y₀,z₀)≠0 Fz′(x0,y0,z0)=0,则有 ∂ z ∂ x = − F x F z , ∂ z ∂ y = − F y F z \dfrac{∂z}{∂x}=-\dfrac{F_x}{F_z},\dfrac{∂z}{∂y}=-\dfrac{F_y}{F_z} ∂x∂z=−FzFx,∂y∂z=−FzFy
例题1:10年2.
分析:公式法。其他两个都视作常数
答案:B
例题2:隐函数 和 复合函数 综合题
解法1:理清变量关系,利用复合函数链式求导法
解法2:全微分形式不变性(优势:不需要分析变量间的关系)
例题3:05年10. 隐函数存在定理
分析: F ( x , y , z ) = x y − z ln y + e x z − 1 F ( 0 , 1 , 1 ) = 0 F(x,y,z)=xy-z\ln y+e^{xz}-1 \qquad F(0,1,1)=0 F(x,y,z)=xy−zlny+exz−1F(0,1,1)=0
F x ( x , y , z ) = y + z e x z F x ( 0 , 1 , 1 ) = 2 ≠ 0 F_x(x,y,z)=y+ze^{xz} \qquad F_x(0,1,1)=2≠0 Fx(x,y,z)=y+zexzFx(0,1,1)=2=0 恒能唯一确定一个连续且具有连续偏导数的隐函数 x = f ( y , z ) x=f(y,z) x=f(y,z)
F y ( x , y , z ) = x − z y F y ( 0 , 1 , 1 ) = − 1 ≠ 0 F_y(x,y,z)=x-\dfrac{z}{y} \qquad F_y(0,1,1)=-1≠0 Fy(x,y,z)=x−yzFy(0,1,1)=−1=0 恒能唯一确定一个连续且具有连续偏导数的隐函数 y = f ( x , z ) y=f(x,z) y=f(x,z)
F z ( x , y , z ) = ln y + x e x z F z ( 0 , 1 , 1 ) = 0 F_z(x,y,z)=\ln y +xe^{xz} \qquad F_z(0,1,1)=0 Fz(x,y,z)=lny+xexzFz(0,1,1)=0 无法作为分母,不能确定有存在连续偏导数的隐函数z=f(x,y)
答案:D
(七) 多元极值
1.无条件极值
(1)二元函数 z = f ( x , y ) z=f(x,y) z=f(x,y)极值存在的必要条件:驻点
满足 { f x ′ ( x 0 , y 0 ) = 0 f y ′ ( x 0 , y 0 ) = 0 \left\{\begin{aligned} f’_x(x_0,y_0)=0 \\ f’_y(x_0,y_0)=0 \end{aligned}\right. {
fx′(x0,y0)=0fy′(x0,y0)=0 的(x,y)为 z=f(x,y)的驻点
可能取得极值的点:
①驻点 : f x ′ = 0 且 f y ′ = 0 f’_x=0且f’_y=0 fx′=0且fy′=0 【若f(x,y)可导,则极值一定是驻点】
②偏导数不存在的点:
i.偏导数均不存在的点:f’x不存在且f’y不存在
ii.对x偏导为0,对y偏导不存在:f’x=0且f’y不存在
iii.对x偏导不存在,对y偏导为0:f’x不存在且f’y=0
(2)二元函数 z = f ( x , y ) z=f(x,y) z=f(x,y)极值存在的充分条件: A C − B 2 > 0 AC-B² > 0 AC−B2>0
①必要条件: ( x 0 , y 0 ) (x_0,y_0) (x0,y0)是驻点,即 f x ( x 0 , y 0 ) = f y ( x 0 , y 0 ) = 0 f_x(x_0,y_0)=f_y(x_0,y_0)=0 fx(x0,y0)=fy(x0,y0)=0
②充分条件:令 A = f x x ( x 0 , y 0 ) , B = f x y ( x 0 , y 0 ) , C = f y y ( x 0 , y 0 ) A=f_{xx}(x_0,y_0),B=f_{xy}(x_0,y_0),C=f_{yy}(x_0,y_0) A=fxx(x0,y0),B=fxy(x0,y0),C=fyy(x0,y0)
i. AC-B²>0,是极值点。A>0 极小值,A<0 极大值
ii. AC-B²<0,不是极值点
iii. AC-B²=0,不定。可能有极值,可能无极值,还需另作讨论。用定义判定 【23年】
例题1:11年3. 二元无条件极值
分析:
法一:极小值,则为凹,笑脸, f ′ ′ ( x 0 ) > 0 f”(x_0)>0 f′′(x0)>0。排除BD
法二:二元极值
①必要条件: ∂ z ∂ x ∣ 0 , 0 = f ′ ( x ) ln f ( y ) ∣ ( 0 , 0 ) = 0 , ∂ z ∂ y ∣ ( 0 , 0 ) = f ( x ) f ′ ( y ) f ( y ) ∣ ( 0 , 0 ) = 0 \dfrac{∂z}{∂x}|_{0,0}=f'(x)\ln f(y)|_{(0,0)}=0,\dfrac{∂z}{∂y}|_{(0,0)}=f(x)\dfrac{f'(y)}{f(y)}|_{(0,0)}=0 ∂x∂z∣0,0=f′(x)lnf(y)∣(0,0)=0,∂y∂z∣(0,0)=f(x)f(y)f′(y)∣(0,0)=0。是驻点,满足必要条件。
②充分条件:令 A = f x x ( x 0 , y 0 ) ∣ ( 0 , 0 ) = f ′ ′ ( 0 ) ln f ( 0 ) , B = f x y ( 0 , 0 ) = f ′ ( x 0 ) f ′ ( y 0 ) f ( y 0 ) ∣ ( 0 , 0 ) = 0 , C = f y y ( x 0 , y 0 ) = f ( x 0 ) f ′ ′ ( y 0 ) f ( y 0 ) − f ′ 2 ( y ) f 2 ( y 0 ) ∣ ( 0 , 0 ) = f ′ ′ ( 0 ) f ( 0 ) A=f_{xx}(x_0,y_0)|_{(0,0)}=f”(0)\ln f(0),B=f_{xy}(0,0)=f'(x_0)\dfrac{f'(y_0)}{f(y_0)}|_{(0,0)}=0,C=f_{yy}(x_0,y_0)=f(x_0)\dfrac{f”(y_0)f(y_0)-f’^2(y)}{f^2(y_0)}|_{(0,0)}=\dfrac{f”(0)}{f(0)} A=fxx(x0,y0)∣(0,0)=f′′(0)lnf(0),B=fxy(0,0)=f′(x0)f(y0)f′(y0)∣(0,0)=0,C=fyy(x0,y0)=f(x0)f2(y0)f′′(y0)f(y0)−f′2(y)∣(0,0)=f(0)f′′(0)
有极值,AC-B²>0,则 f ′ ′ 2 ( 0 ) ln f ( 0 ) f ( 0 ) > 0 \dfrac{f”^2(0)\ln f(0)}{f(0)}>0 f(0)f′′2(0)lnf(0)>0,∵f(x)>0 ∴lnf(0)>0,即f(0)>1
且因是极小值, A = f ′ ′ ( 0 ) l n f ( 0 ) > 0 , ∴ f ′ ′ ( 0 ) > 0 A=f”(0)lnf(0)>0,∴f”(0)>0 A=f′′(0)lnf(0)>0,∴f′′(0)>0
答案:A
2.条件极值
(1)代入法
化条件极值为无条件极值
①直角坐标
②圆、椭圆:参数方程
(2)拉格朗日乘数法
1.二元函数z=f(x,y)的条件极值
要找二元函数 z=f(x,y)在附加条件φ(x,y)=0下可能的极值点:
①构造拉格朗日函数 L ( x , y , λ ) = f ( x , y ) + λ φ ( x , y ) L(x,y,λ)=f(x,y)+λφ(x,y) L(x,y,λ)=f(x,y)+λφ(x,y)
②对每个参数求一阶偏导: { L x = f x ( x , y ) + λ φ x ( x , y ) = 0 L y = f y ( x , y ) + λ φ y ( x , y ) = 0 L λ = φ ( x , y ) = 0 \left\{\begin{aligned} {\rm L}_x & = f_x(x,y)+λφ_x(x,y) = 0 \\ {\rm L}_y & = f_y(x,y)+λφ_y(x,y) = 0 \\ {\rm L}_λ & = φ(x,y) = 0 \\ \end{aligned}\right. ⎩
⎨
⎧LxLyLλ=fx(x,y)+λφx(x,y)=0=fy(x,y)+λφy(x,y)=0=φ(x,y)=0
③解方程组,得到可能的极值点
2.三元函数u=f(x,y,z)的条件极值
要找三元函数 u=f(x,y,z)在附加条件φ(x,y,z)=0下可能的极值点:
①构造拉格朗日函数 L ( x , y , z , λ ) = f ( x , y , z ) + λ φ ( x , y , z ) L(x,y,z,λ)=f(x,y,z)+λφ(x,y,z) L(x,y,z,λ)=f(x,y,z)+λφ(x,y,z)
②对每个参数求一阶偏导: { L x = f x ( x , y , z ) + λ φ x ( x , y , z ) = 0 L y = f y ( x , y , z ) + λ φ y ( x , y , z ) = 0 L z = f z ( x , y , z ) + λ φ z ( x , y , z ) = 0 L λ = φ ( x , y , z ) = 0 \left\{\begin{aligned} {\rm L}_x & = f_x(x,y,z)+λφ_x(x,y,z) = 0 \\ {\rm L}_y & = f_y(x,y,z)+λφ_y(x,y,z) = 0 \\ {\rm L}_z & = f_z(x,y,z)+λφ_z(x,y,z) = 0 \\ {\rm L}_λ & = φ(x,y,z) = 0 \\ \end{aligned}\right. ⎩
⎨
⎧LxLyLzLλ=fx(x,y,z)+λφx(x,y,z)=0=fy(x,y,z)+λφy(x,y,z)=0=fz(x,y,z)+λφz(x,y,z)=0=φ(x,y,z)=0
③解方程组,得到可能的极值点
例题1:15年17.
例题2:18年16. 拉格朗日乘数法求条件极值:应用题
答案:
例题3:08年数二 条件极值:三元函数+两个条件
答案:
3.二元函数在有界闭区域上的最值
求二元函数在有界闭区域上的最值的3步骤:
①先求闭区域D内部各驻点的函数值
②闭区域D 边界的最大最小值
③驻点值与边界最值比大小,最大的为最大值,最小的为最小值
例题1:22年13.
分析:
答案: [ 4 e − 2 , + ∞ ) [4e^{-2},+∞) [4e−2,+∞)
例题3:03年9. 二元极值
分析:
答案:A
例题4:07年17. 条件极值:不用求二阶导,只比较驻点函数值与边界函数值的大小
分析:
(八) 多元微分的几何应用
1.曲面的法向量 n ⃗ \vec{n} n、法线、切平面
1.曲面方程: F ( x , y , z ) = 0 F(x,y,z)=0 F(x,y,z)=0,切点 ( x 0 , y 0 , z 0 ) (x_0,y_0,z_0) (x0,y0,z0):
①曲面的法向量 n ⃗ = { F x ′ , F y ′ , F z ′ } ∣ ( x 0 , y 0 , z 0 ) \vec{n}=\{F’_x,F’_y,F’_z\}|_{(x_0,y_0,z_0)} n={
Fx′,Fy′,Fz′}∣(x0,y0,z0)
②曲面的法线方程: x − x 0 F x ′ ( x 0 , y 0 , z 0 ) = y − y 0 F y ′ ( x 0 , y 0 , z 0 ) = z − z 0 F z ′ ( x 0 , y 0 , z 0 ) \dfrac{x-x_0}{F’_x(x_0,y_0,z_0)}=\dfrac{y-y_0}{F’_y(x_0,y_0,z_0)}=\dfrac{z-z_0}{F’_z(x_0,y_0,z_0)} Fx′(x0,y0,z0)x−x0=Fy′(x0,y0,z0)y−y0=Fz′(x0,y0,z0)z−z0
③切平面方程可表示为: F x ′ ( x 0 , y 0 , z 0 ) ( x − x 0 ) + F y ′ ( x 0 , y 0 , z 0 ) ( y − y 0 ) + F z ′ ( x 0 , y 0 , z 0 ) ( z − z 0 ) = 0 F’_x(x_0,y_0,z_0)(x-x_0)+F’_y(x_0,y_0,z_0)(y-y_0)+F’_z(x_0,y_0,z_0)(z-z_0)=0 Fx′(x0,y0,z0)(x−x0)+Fy′(x0,y0,z0)(y−y0)+Fz′(x0,y0,z0)(z−z0)=0
2.曲面方程: z = f ( x , y ) z=f(x,y) z=f(x,y),切点 ( x 0 , y 0 , z 0 ) (x_0,y_0,z_0) (x0,y0,z0):
①法向量: n ⃗ = { f x ′ , f y ′ , − 1 } \vec{n}=\{f’_x,f’_y,-1\} n={
fx′,fy′,−1}
②法线: x − x 0 f x ′ ( x 0 , y 0 , z 0 ) = y − y 0 f y ′ ( x 0 , y 0 , z 0 ) = z − z 0 − 1 \dfrac{x-x_0}{f’_x(x_0,y_0,z_0)}=\dfrac{y-y_0}{f’_y(x_0,y_0,z_0)}=\dfrac{z-z_0}{-1} fx′(x0,y0,z0)x−x0=fy′(x0,y0,z0)y−y0=−1z−z0
③切平面: f x ′ ( x 0 , y 0 ) ( x − x 0 ) + f y ′ ( x 0 , y 0 ) ( y − y 0 ) − ( z − z 0 ) = 0 f’_x(x_0,y_0)(x-x_0)+f’_y(x_0,y_0)(y-y_0)-(z-z_0)=0 fx′(x0,y0)(x−x0)+fy′(x0,y0)(y−y0)−(z−z0)=0
例题1:13年2. 求切平面方程:先求法向量
分析:求切平面,先求法向量
F ( x , y , z ) = x 2 + c o s ( x y ) + y z + x = 0 F(x,y,z)=x^2+cos(xy)+yz+x=0 F(x,y,z)=x2+cos(xy)+yz+x=0,求出对应 F x , F y , F z F_x,F_y,F_z Fx,Fy,Fz,并代入点(0,1,-1)。
得切平面方程: F x ( x − x 0 ) + F y ( y − y 0 ) + F z ( z − z 0 ) = 0 F_x(x-x_0)+F_y(y-y_0)+F_z(z-z_0)=0 Fx(x−x0)+Fy(y−y0)+Fz(z−z0)=0
答案:A
例题2:14年9.
分析:已知切点,只需要求法向量,即可点法式得切平面方程
z=f(x,y),曲面法向量为 n ⃗ = ( f x , f y , − 1 ) \vec{n}=(f_x,f_y,-1) n=(fx,fy,−1) ,切点为(1,0,1)
【f(x,y)较复杂,求偏导考虑先代后求:求谁谁不动,其他字母代数值】
f ( x , y ) = x 2 ( 1 − s i n y ) + y 2 ( 1 − s i n x ) f(x,y)=x^2(1-siny)+y^2(1-sinx) f(x,y)=x2(1−siny)+y2(1−sinx)
f ( x , 0 ) = x 2 , f x = 2 x ∣ ( 1 , 0 ) = 2 f(x,0)=x^2,f_x=2x|_{(1,0)}=2 f(x,0)=x2,fx=2x∣(1,0)=2
f ( 1 , y ) = 1 − s i n y + y 2 ( 1 − s i n 1 ) , f y = − c o s y + 2 y ( 1 − s i n 1 ) ∣ ( 1 , 0 ) = − 1 f(1,y)=1-siny+y^2(1-sin1),f_y=-cosy+2y(1-sin1)|_{(1,0)}=-1 f(1,y)=1−siny+y2(1−sin1),fy=−cosy+2y(1−sin1)∣(1,0)=−1
∴ n ⃗ = ( 2 , − 1 , − 1 ) \vec{n}=(2,-1,-1) n=(2,−1,−1)
∴切平面方程:2(x-1)-y-(z-1)=0,即2x-y-z-1=0
答案: 2 x − y − z − 1 = 0 2x-y-z-1=0 2x−y−z−1=0
例题3:03年2.
分析:点法式,求法向量和切点
曲面z=f(x,y),法向量为 n 1 ⃗ = ( f x , f y , − 1 ) = ( 2 x 0 , 2 y 0 , − 1 ) \vec{n_1}=(f_x,f_y,-1)=(2x_0,2y_0,-1) n1=(fx,fy,−1)=(2x0,2y0,−1)。平面法向量 n 2 ⃗ = ( 2 , 4 , − 1 ) \vec{n_2}=(2,4,-1) n2=(2,4,−1)
与平面平行,则两者法向量成比例,即 2 x 0 2 = 2 y 0 4 = − 1 − 1 = 1 \dfrac{2x_0}{2}=\dfrac{2y_0}{4}=\dfrac{-1}{-1}=1 22x0=42y0=−1−1=1,∴ x 0 = 1 , y 0 = 2 , z 0 = 5 x_0=1,y_0=2,z_0=5 x0=1,y0=2,z0=5
∴曲面法向量为(2,4,-1),切点(1,2,5),求点法式得切平面方程:2(x-1)+4(y-2)-(z-5)=2x+4y-z-5=0
答案: 2 x + 4 y − z − 5 = 0 2x+4y-z-5=0 2x+4y−z−5=0
例题4:18年2.
分析:
法一:直接法,求切点
难点在于找切点,需要联立三个方程
法二:排除法
切平面过(1,0,0)、(0,1,0),不满足x=y,排除C、D
根据法向量平行,排除A
答案:B
例题5:00年2. 求曲面的法线方程
分析:法线方程,同样只需要切点和法向量
①切点已知为(1-2,2)
②曲面的法向量 n ⃗ = { F x ( x 0 , y 0 , z 0 ) , F y ( x 0 , y 0 , z 0 ) , F z ( x 0 , y 0 , z 0 ) } = { 2 x , 4 y , 6 z } ∣ ( 1 , − 2 , 2 ) = { 2 , − 8 , 12 } \vec{n}=\{F_x(x_0,y_0,z_0),F_y(x_0,y_0,z_0),F_z(x_0,y_0,z_0)\}=\{2x,4y,6z\}|_{(1,-2,2)}=\{2,-8,12\} n={
Fx(x0,y0,z0),Fy(x0,y0,z0),Fz(x0,y0,z0)}={
2x,4y,6z}∣(1,−2,2)={
2,−8,12},可取 n ⃗ = ( 1 , − 4 , 6 ) \vec{n}=(1,-4,6) n=(1,−4,6)
③曲面的法线方程: x − 1 2 = y + 2 − 8 = z − 2 12 \dfrac{x-1}{2}=\dfrac{y+2}{-8}=\dfrac{z-2}{12} 2x−1=−8y+2=12z−2,即 x − 1 1 = y + 2 − 4 = z − 2 6 \dfrac{x-1}{1}=\dfrac{y+2}{-4}=\dfrac{z-2}{6} 1x−1=−4y+2=6z−2
答案: x − 1 1 = y + 2 − 4 = z − 2 6 \dfrac{x-1}{1}=\dfrac{y+2}{-4}=\dfrac{z-2}{6} 1x−1=−4y+2=6z−2
2.曲线的切向量 τ ⃗ \vec{τ} τ、切线、法平面
例题1:求曲线的切线方程和法平面方程,还是要求切点和切向量
分析:切点 ( π 2 − 1 , 1 , 2 2 ) (\dfrac{π}{2}-1,1,2\sqrt{2}) (2π−1,1,22),切向量 ( 1 , 1 , 2 ) (1,1,\sqrt{2}) (1,1,2)
答案:
例题2:已知切点,求切向量
分析:对于交面式, τ ⃗ = n 1 ⃗ × n 2 ⃗ \vec{τ}=\vec{n_1}×\vec{n_2} τ=n1×n2
n 1 ⃗ = ( 2 , − 4 , 2 ) \vec{n_1}=(2,-4,2) n1=(2,−4,2), n 2 ⃗ = ( 1 , 1 , 1 ) \vec{n_2}=(1,1,1) n2=(1,1,1)
τ ⃗ = n 1 ⃗ × n 2 ⃗ = ( − 6 , 0 , 6 ) \vec{τ}=\vec{n_1}×\vec{n_2}=(-6,0,6) τ=n1×n2=(−6,0,6) ,可取 τ ⃗ = ( − 3 , 0 , 3 ) \vec{τ}=(-3,0,3) τ=(−3,0,3)
答案:
例题3:01年7.
分析:
A.偏导数存在,不一定可微 A❌
B.法向量为 (3,1,-1) B❌
对于C, { F ( x , y , z ) = f ( x , y ) − z = 0 G ( x , y , z ) = y = 0 \left\{\begin{aligned} F(x,y,z) & = f(x,y)-z = 0\\ G(x,y,z) & = y = 0 \end{aligned}\right. {
F(x,y,z)G(x,y,z)=f(x,y)−z=0=y=0
n 1 ⃗ = ( f x , f y , − 1 ) = ( 3 , 1 , − 1 ) \vec{n_1}=(f_x,f_y,-1)=(3,1,-1) n1=(fx,fy,−1)=(3,1,−1), n 2 ⃗ = ( 0 , 1 , 0 ) \vec{n_2}=(0,1,0) n2=(0,1,0)
∴切向量 τ ⃗ = n 1 ⃗ × n 2 ⃗ = ( 1 , 0 , 3 ) \vec{τ}=\vec{n_1}×\vec{n_2}=(1,0,3) τ=n1×n2=(1,0,3)
答案:C
例题4:23李林六套卷(二) 11.
分析:
①切点:(1,1,0)
②求切向量:
{ F ( x , y , z ) = − x + y 2 = 0 G ( x , y , z ) = 3 ( y − 1 ) − z = 3 y − 3 − z = 0 \left\{\begin{aligned} F(x,y,z) & = -x+y^2 = 0\\ G(x,y,z) & = 3(y-1)-z =3y-3-z= 0 \end{aligned}\right. {
F(x,y,z)G(x,y,z)=−x+y2=0=3(y−1)−z=3y−3−z=0
n 1 ⃗ = ( − 1 , 2 y , 0 ) ∣ ( 1 , 1 , 0 ) = ( − 1 , 2 , 0 ) \vec{n_1}=(-1,2y,0)|_{(1,1,0)}=(-1,2,0) n1=(−1,2y,0)∣(1,1,0)=(−1,2,0)
n 2 ⃗ = ( 0 , 3 , − 1 ) \vec{n_2}=(0,3,-1) n2=(0,3,−1)
∴切向量 τ ⃗ = n 1 ⃗ × n 2 ⃗ = ( − 2 , − 1 , − 3 ) \vec{τ}=\vec{n_1}×\vec{n_2}=(-2,-1,-3) τ=n1×n2=(−2,−1,−3),可取 τ ⃗ = ( 2 , 1 , 3 ) \vec{τ}=(2,1,3) τ=(2,1,3)
答案: x − 1 2 = y − 1 1 = z 3 \dfrac{x-1}{2}=\dfrac{y-1}{1}=\dfrac{z}{3} 2x−1=1y−1=3z
(九) 方向导数与梯度
1.方向导数 ∂ f ∂ l \dfrac{∂f}{∂l} ∂l∂f
1.定义
∂ f ∂ l ∣ ( x 0 , y 0 ) = lim t → 0 + f ( x 0 + t cos α , y 0 + t cos β ) − f ( x 0 , y 0 ) t \dfrac{∂f}{∂l}|_{(x_0,y_0)}=\lim\limits_{t→0^+}\dfrac{f(x_0+t\cosα,y_0+t\cosβ)-f(x_0,y_0)}{t} ∂l∂f∣(x0,y0)=t→0+limtf(x0+tcosα,y0+tcosβ)−f(x0,y0)
2.计算
(1)二元方向导数:若 z = f ( x , y ) z=f(x,y) z=f(x,y)可微 (充分条件),则 ∂ f ∂ l ∣ ( x 0 , y 0 ) = ∂ f ∂ x cos α + ∂ f ∂ y cos β ∣ ( x 0 , y 0 ) \dfrac{∂f}{∂l}|_{(x_0,y_0)}=\dfrac{∂f}{∂x}\cosα+\dfrac{∂f}{∂y}\cosβ|_{(x_0,y_0)} ∂l∂f∣(x0,y0)=∂x∂fcosα+∂y∂fcosβ∣(x0,y0)
(2)三元方向导数: ∂ f ∂ l ∣ ( x 0 , y 0 , z 0 ) = ∂ f ∂ x cos α + ∂ f ∂ y cos β + ∂ f ∂ z cos γ ∣ ( x 0 , y 0 , z 0 ) \dfrac{∂f}{∂l}|_{(x_0,y_0,z_0)}=\dfrac{∂f}{∂x}\cosα+\dfrac{∂f}{∂y}\cosβ+\dfrac{∂f}{∂z}\cosγ|_{(x_0,y_0,z_0)} ∂l∂f∣(x0,y0,z0)=∂x∂fcosα+∂y∂fcosβ+∂z∂fcosγ∣(x0,y0,z0)
3.几何意义:
①导数:刻画一元函数的变化率
②偏导数:对x的偏导数 f x f_x fx刻画二元函数 f ( x , y ) f(x,y) f(x,y)沿 x x x轴的变化率,对y的偏导数 f y f_y fy刻画二元函数 f ( x , y ) f(x,y) f(x,y)沿 y y y轴的变化率
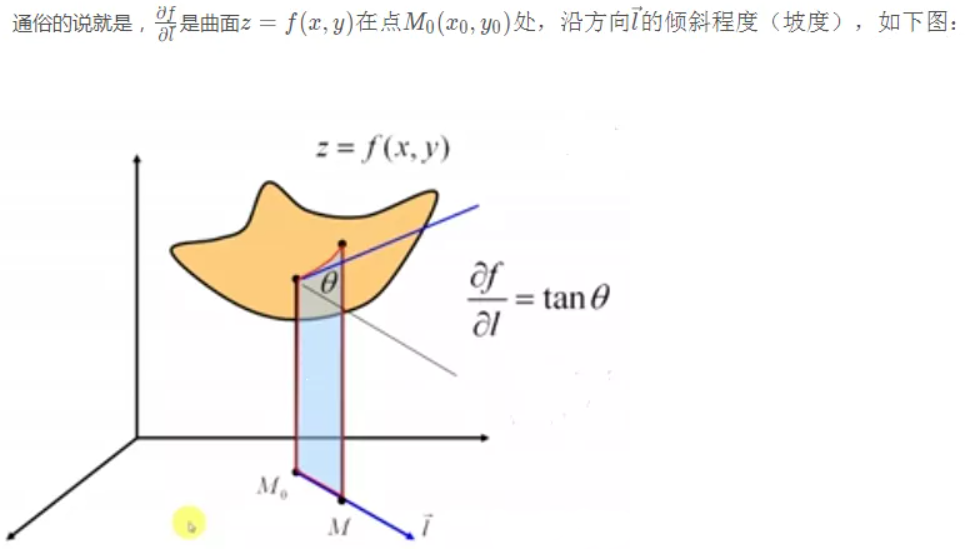
③方向导数:为了刻画多元函数沿任意给定方向 l ⃗ \vec{l} l的变化率(坡度),引入了方向导数。
4.方向导数的几何意义:向量 l ⃗ \vec{l} l与曲面 z = f ( x , y ) z=f(x,y) z=f(x,y)的交线,沿着 l ⃗ \vec{l} l方向的切线的斜率。
特别的, f ( x , y ) f(x,y) f(x,y)在点 M 0 ( x 0 , y 0 ) M_0(x_0,y_0) M0(x0,y0)处对x的偏导数存在,且 f x ( x 0 , y 0 ) = a f_x(x_0,y_0)=a fx(x0,y0)=a,则:
f ( x , y ) f(x,y) f(x,y)在点 M 0 ( x 0 , y 0 ) M_0(x_0,y_0) M0(x0,y0)处沿x轴正方向的方向导数为 a a a,沿x轴负方向的方向导数为 − a -a −a
y y y轴同理。
方向导数
例题1:05年3. 方向导数
分析:
答案: 3 3 \dfrac{\sqrt{3}}{3} 33
例题2:17年3.
分析:
答案:D
2.梯度 g r a d \rm grad grad
梯度是一个向量:
二元梯度: g r a d ⃗ f ( x 0 , y 0 ) = ∂ f ∂ x i ⃗ + ∂ f ∂ y j ⃗ ∣ ( x 0 , y 0 ) = f x ′ i ⃗ + f y ′ j ⃗ ∣ ( x 0 , y 0 ) \vec{\rm grad}f(x_0,y_0)=\dfrac{∂f}{∂x}\vec{i}+\dfrac{∂f}{∂y}\vec{j}|_{(x_0,y_0)}=f’_x\vec{i}+f’_y\vec{j}|_{(x_0,y_0)} gradf(x0,y0)=∂x∂fi+∂y∂fj∣(x0,y0)=fx′i+fy′j∣(x0,y0)
二元梯度的模: ∣ g r a d f ∣ ⃗ = ( ∂ f ∂ x ) 2 + ( ∂ f ∂ y ) 2 = f x ′ 2 + f y ′ 2 |\vec{\rm gradf|}=\sqrt{(\dfrac{∂f}{∂x})^2+(\dfrac{∂f}{∂y})^2}=\sqrt{f’^2_x+f’^2_y} ∣gradf∣=(∂x∂f)2+(∂y∂f)2=fx′2+fy′2 【15年17.】
三元梯度: g r a d ⃗ f ( x 0 , y 0 , z 0 ) = ∂ f ∂ x i ⃗ + ∂ f ∂ y j ⃗ + ∂ f ∂ z k ⃗ ∣ ( x 0 , y 0 , z 0 ) = f x ′ i ⃗ + f y ′ j ⃗ + f z ′ k ⃗ ∣ ( x 0 , y 0 , z 0 ) \vec{\rm grad}f(x_0,y_0,z_0)=\dfrac{∂f}{∂x}\vec{i}+\dfrac{∂f}{∂y}\vec{j}+\dfrac{∂f}{∂z}\vec{k}|_{(x_0,y_0,z_0)}=f’_x\vec{i}+f’_y\vec{j}+f’_z\vec{k}|_{(x_0,y_0,z_0)} gradf(x0,y0,z0)=∂x∂fi+∂y∂fj+∂z∂fk∣(x0,y0,z0)=fx′i+fy′j+fz′k∣(x0,y0,z0)
三元梯度的模: ∣ g r a d f ∣ ⃗ = ( ∂ f ∂ x ) 2 + ( ∂ f ∂ y ) 2 + ( ∂ f ∂ z ) 2 = f x ′ 2 + f y ′ 2 + f z ′ 2 |\vec{\rm gradf|}=\sqrt{(\dfrac{∂f}{∂x})^2+(\dfrac{∂f}{∂y})^2+(\dfrac{∂f}{∂z})^2}=\sqrt{f’^2_x+f’^2_y+f’^2_z} ∣gradf∣=(∂x∂f)2+(∂y∂f)2+(∂z∂f)2=fx′2+fy′2+fz′2
例题1:12年11. 梯度就是 i ⃗ , j ⃗ , k ⃗ \vec{i},\vec{j},\vec{k} i,j,k
分析: f x ′ = y , f y ′ = x − z y 2 , f z ′ = 1 y f’_x=y,f’_y=x-\dfrac{z}{y^2},f’_z=\dfrac{1}{y} fx′=y,fy′=x−y2z,fz′=y1
g r a d ⃗ f ∣ ( 2 , 1 , 1 ) = f x ′ i ⃗ + f y ′ j ⃗ + f z ′ k ⃗ ∣ ( 2 , 1 , 1 ) = i ⃗ + j ⃗ + k ⃗ = ( 1 , 1 , 1 ) \vec{grad}f|_{(2,1,1)}=f’_x\vec{i}+f’_y\vec{j}+f’_z\vec{k}|_{(2,1,1)}=\vec{i}+\vec{j}+\vec{k}=(1,1,1) gradf∣(2,1,1)=fx′i+fy′j+fz′k∣(2,1,1)=i+j+k=(1,1,1)
答案: i ⃗ + j ⃗ + k ⃗ \vec{i}+\vec{j}+\vec{k} i+j+k 或 ( 1 , 1 , 1 ) (1,1,1) (1,1,1)
3.方向导数与梯度的关系
1.最大方向导数 (方向导数的最大值) = 梯度的模 = ∣ g r a d f ∣ ⃗ = ( ∂ f ∂ x ) 2 + ( ∂ f ∂ y ) 2 = f x ′ 2 + f y ′ 2 =|\vec{\rm gradf|}=\sqrt{(\dfrac{∂f}{∂x})^2+(\dfrac{∂f}{∂y})^2}=\sqrt{f’^2_x+f’^2_y} =∣gradf∣=(∂x∂f)2+(∂y∂f)2=fx′2+fy′2
2. f ( x , y ) f(x,y) f(x,y)在点 ( a , b ) (a,b) (a,b)沿 l ⃗ = ( c , d ) \vec{l}=(c,d) l=(c,d)的方向导数,取得最大值e:
①沿 l ⃗ = ( c , d ) \vec{l}=(c,d) l=(c,d):与 l ⃗ = ( 0 , 1 ) \vec{l}=(0,1) l=(0,1)同向,即 f x ′ ( a , b ) c = f y ′ ( a , b ) d > 0 \dfrac{f’_x(a,b)}{c}=\dfrac{f’_y(a,b)}{d}>0 cfx′(a,b)=dfy′(a,b)>0
②取得最大值e: ∣ ∣ g r a d f ( a , b ) ∣ ∣ = ( f x ′ ( a , b ) ) 2 + ( f y ′ ( a , b ) ) 2 = e ||gradf(a,b)||=\sqrt{(f’_x(a,b))^2+(f’_y(a,b))^2}=e ∣∣gradf(a,b)∣∣=(fx′(a,b))2+(fy′(a,b))2=e
①梯度是一个向量:梯度的方向是方向导数最大的方向,梯度的模是方向导数的最大值】
②函数沿着梯度方向的方向导数最大,函数在一点处的方向导数的最大值 等于 函数在该点的梯度的模【15年17.】
例题1:22年11. 方向导数与梯度的关系:最大方向导数为梯度的模长
分析:最大方向导数为梯度的模长
答案:4
例题2:19年16(1). 方向导数与梯度的关系、第一类曲面积分
答案:
例题3:24李林六(二)1.
分析:沿 l ⃗ = ( 0 , 1 ) \vec{l}=(0,1) l=(0,1):与 l ⃗ = ( 0 , 1 ) \vec{l}=(0,1) l=(0,1)同向,即 f x ′ 0 = f y ′ 1 > 0 \dfrac{f’_x}{0}=\dfrac{f’_y}{1}>0 0fx′=1fy′>0
答案:C
例题4:15年17.
(十) 二元泰勒公式:泰勒多项式
背住第二行的公式即可:
①先求出 f ( x 0 , y 0 ) f(x_0,y_0) f(x0,y0)、 f x ′ ( x 0 , y 0 ) f_x'(x_0,y_0) fx′(x0,y0)、 f y ′ ( x 0 , y 0 ) f_y'(x_0,y_0) fy′(x0,y0)、 f x x ′ ′ ( x 0 , y 0 ) f_{xx}”(x_0,y_0) fxx′′(x0,y0)、 f x y ′ ′ ( x 0 , y 0 ) f_{xy}”(x_0,y_0) fxy′′(x0,y0)、 f y y ′ ′ ( x 0 , y 0 ) f_{yy}”(x_0,y_0) fyy′′(x0,y0)
②代入公式即可
例题1:23李林四(三)13.
分析:
答案:5+2(x-1)²-(x-1)(y+2)-(y+2)²
今天的文章高数第九章多元函数微分法及其应用_高数一元函数微分数题与解析分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/83656.html